Сначала запишем формулы, которые понадобятся:
Площадь квадрата равна квадрату его стороны:
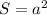
Отсюда, сторона квадрата равна корню квадратному из площади:

Периметр квадрата равен четырём его сторонам:

Подставим в эту формулу вместо стороны a корень из площади, и мы получим вот что:
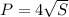
Так считается периметр для квадрата с площадью S
А если взять площадь в девять раз больше (то есть 9S ), то получим периметр P₂ , который равен:
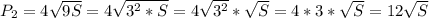
Во сколько раз увеличился периметр? Поделим новый периметр на старый, и узнаем (хоть это и так тут уже понятно).
Периметр увеличился в:
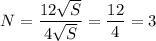 (раза)
(раза)
ответ: периметр увеличится в 3 раза
а) 6²+8²=10²
б) 5²+6² ≠ 7²
в) 9²+12²=15²
Отсюда ⇒ треугольник является прямоугольным в случаях: а и в.
Треугольник прямоугольный, если сумма квадратов меньших сторон равна квадрату большей.
Удачи!