С первым числом все понятно: оно заканчивается цифрой 5, поскольку любое число, заканчивающееся пятеркой, в любой степени тоже будет заканчиваться цифрой 5.
Со вторым - аналогично: любое число, заканчивающееся шестеркой, в любой степени тоже будет заканчиваться цифрой 6.
С третьим - немного сложнее. Посмотрим, какой цифрой могут заканчиваться степени числа 2017:
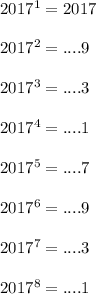
и т.д.. Т.е. последнии цифры степеней числа 2017 чередуются в таком порядке - 7, 9, 3, 1 - и повторяются с интервалом в 4 цифры.
Поскольку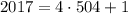 
, то последняя цифра числа 
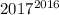- единица. Тогда последняя цифра числа 
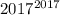- семерка.
Ну а если первое число заканчивается 5, второе - 6, третье - 7, то выражение заканчивается последней цифрой суммы последних цифр всех трех степеней: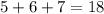 
- значит, значение выражения заканчивается цифрой 8.
Основные функции
\left(a=\operatorname{const} \right)
x^{a}: x^a
модуль x: abs(x)
\sqrt{x}: Sqrt[x]
\sqrt[n]{x}: x^(1/n)
a^{x}: a^x
\log_{a}x: Log[a, x]
\ln x: Log[x]
\cos x: cos[x] или Cos[x]
\sin x: sin[x] или Sin[x]
\operatorname{tg}x: tan[x] или Tan[x]
\operatorname{ctg}x: cot[x] или Cot[x]
\sec x: sec[x] или Sec[x]
\operatorname{cosec} x: csc[x] или Csc[x]
\arccos x: ArcCos[x]
\arcsin x: ArcSin[x]
\operatorname{arctg} x: ArcTan[x]
\operatorname{arcctg} x: ArcCot[x]
\operatorname{arcsec} x: ArcSec[x]
\operatorname{arccosec} x: ArcCsc[x]
\operatorname{ch} x: cosh[x] или Cosh[x]
\operatorname{sh} x: sinh[x] или Sinh[x]
\operatorname{th} x: tanh[x] или Tanh[x]
\operatorname{cth} x: coth[x] или Coth[x]
\operatorname{sech} x: sech[x] или Sech[x]
\operatorname{cosech} x: csch[x] или Csch[е]
\operatorname{areach} x: ArcCosh[x]
\operatorname{areash} x: ArcSinh[x]
\operatorname{areath} x: ArcTanh[x]
\operatorname{areacth} x: ArcCoth[x]
\operatorname{areasech} x: ArcSech[x]
\operatorname{areacosech} x: ArcCsch[x]
[19.67] =19: integral part of (19.67) - выделяет целую часть числа (integerPart)
Пошаговое объяснение: