
В прямоугольной системе координат ху на плоскости задан равнобедренный треугольник АСВ, в котором АС=ВС , а(2:-5), в (4:3). Вокруг этого треугольника описан круг, заданное уравнением (х-3)2+у2+2у=16. Определите площадь треугольника АВС.
Пошаговое объяснение:
Найдем координаты центра окружности О из (х-3)²+у²+2у=16.
(х-3)²+(у²+2у+1)-1=16 ,
(х-3)²+(у+1)²=16+1 ,
(х-3)²+(у+1)²=17 ⇒О(3;-1) , R=√17.
Найдем координаты середины отрезка АВ , точки М( (2+4):2 :(-5+3):2 ) или М(3;-1). Ой координаты точки М и О совпали. Это означает , что это одна точка , пусть ее название О∈АВ.
R=√17, ОА=ОВ=√17 ⇒ ΔАВС-прямоугольный и катеты СА=СВ=х, АВ=2√17 .
По т. Пифагора 2х²=АВ² или 2х²=4 *17 или х=√34.
S=0.5*АС*ВС , S=0,5*√34*√34=17 (ед²)
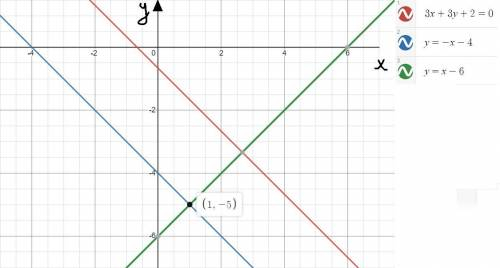
L1: y = -x-4
L2: y = x-6
Пошаговое объяснение:
Дано:
M(1;-5)
L: 3x+3y+2 = 0
Найти: L1, L2
Решение: 1) Для начала выразим прямую L как каноническое уравнение прямой y = kx+b
3x+3y+2 = 0;
3y = -3x-2|:3;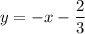
2) Прямые параллельны когда у них меняется свободный член, т.е. k остаётся неизменным, а b нет. Получается коэффициент k у параллельной прямой будет также равен -1
Подставим координаты точки М в каноническое уравнение прямой
-5 = -1*1+b
b = -5+1
b = -4
Уравнение параллельной 3x+3y+2 = 0 прямой, проходящей через точку M(1;-5) будет выглядеть как y = -x-4
3) Для перпендикулярной y = kx+b прямой, проходящей через точку N(x₁,y₁) есть следующая формула:
y-y₁ = -(x-x₁)/k
Получается, перпендикулярная y = -x-²/₃ прямая, проходящая через M(1;-5) будет выглядеть как: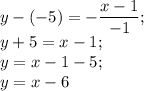
Если построить все данные в одной плоскости, то можно убедиться в правильном нахождении неизвестных прямых(см. вложение)
4,6,6,8,0,4,6,3
Пошаговое объяснение: