Математика: Амалдарды орында: 1/2×3/4×5/6×7/8+93/128

Заметим, что Докажем, что, начиная с , последовательность Фибоначчи периодическая по модулю 1000.Рассмотрим пару чисел .Каждое из чисел каждой из пар дает один из остатков по модулю . Тогда всего вариантов пар остатков от деления на 1000 может быть (1000 вариантов остатков 1ого числа пары и 1000 вариантов у 2ого). Тогда, по принципу Дирихле, в рассматриваемом мн-ве пар найдутся хотя бы 2 пары чисел, соответствующие элементы которых сравнимы по модулю 1000 - а, с учетом определения последовательности...

Амалдарды орында: 1/2×3/4×5/6×7/8+93/128

👇

Увидеть ответ

Ответ:

katarakta

11.11.2022

=5/9

Пошаговое объяснение:

тут это 100% я забыл как решать но у нас было

4,8(34 оценок)

Открыть все ответы

Ответ:

CERN

11.11.2022

НОД (220; 360) = 20.

Как найти наибольший общий делитель для 220 и 360

Разложим на простые множители 220

220 = 2 • 2 • 5 • 11

Разложим на простые множители 360

360 = 2 • 2 • 2 • 3 • 3 • 5

Выберем одинаковые простые множители в обоих числах.

2 , 2 , 5

Находим произведение одинаковых простых множителей и записываем ответ

НОД (220; 360) = 2 • 2 • 5 = 20

НОК (Наименьшее общее кратное) 220 и 360

Наименьшим общим кратным (НОК) 220 и 360 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (220 и 360).

НОК (220, 360) = 3960

Как найти наименьшее общее кратное для 220 и 360

Разложим на простые множители 220

220 = 2 • 2 • 5 • 11

Разложим на простые множители 360

360 = 2 • 2 • 2 • 3 • 3 • 5

Выберем в разложении меньшего числа (220) множители, которые не вошли в разложение

Добавим эти множители в разложение бóльшего числа

2 , 2 , 2 , 3 , 3 , 5 , 11

Полученное произведение запишем в ответ.

НОК (220, 360) = 2 • 2 • 2 • 3 • 3 • 5 • 11 = 3960

4,4(14 оценок)

Ответ:

Aleksandra00123

11.11.2022

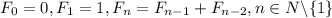
$F_0=0,F_1=1, F_n=F_{n-1}+F_{n-2}, n\in N\backslash\{1\}$

Заметим, что 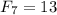F_7=13

Докажем, что, начиная с 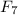F_7 , последовательность Фибоначчи периодическая по модулю 1000.

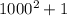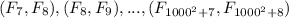Рассмотрим 1000^2+1 пару чисел $(F_7,F_8),(F_8,F_9),...,(F_{1000^2+7},F_{1000^2+8})$ .

Каждое из чисел каждой из пар дает один из 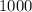1000 остатков по модулю 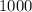1000 . Тогда всего вариантов пар остатков от деления на 1000 может быть 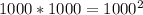1000*1000=1000^2 (1000 вариантов остатков 1ого числа пары и 1000 вариантов у 2ого).

Тогда, по принципу Дирихле, в рассматриваемом мн-ве пар найдутся хотя бы 2 пары чисел, соответствующие элементы которых сравнимы по модулю 1000 - а, с учетом определения последовательности Фибоначчи, это и означает периодичность остатков ее членов по модулю 1000.

Возьмем 2 такие пары с наименьшими номерами. Пусть это пары 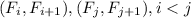$(F_i,F_{i+1}), (F_j,F_{j+1}), i$ . Покажем, что i=7 .

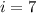Пусть не так, и .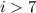

По построению, 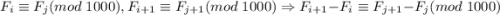$F_i\equiv F_j(mod \;1000),F_{i+1}\equiv F_{j+1}(mod \;1000)\Rightarrow F_{i+1}-F_{i}\equiv F_{j+1}-F_{j}(mod \;1000)$

Но, по определению последовательности Фибоначчи, 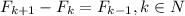$F_{k+1}-F_{k}=F_{k-1},k\in N$ . А значит 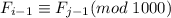$F_{i-1}\equiv F_{j-1}(mod\; 1000)$ . А тогда соответствующие элементы пар чисел 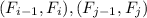$(F_{i-1},F_i),(F_{j-1},F_j)$ сравнимы по модулю 1000 - противоречие с тем, что 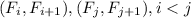$(F_i,F_{i+1}), (F_j,F_{j+1}), i$ - пары с наименьшими номерами.

Значит 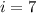i=7 .

А это означает, что в последовательности остатков от деления членов последовательности Фибоначчи на 1000 найдется сколь угодно чисел, сравнимых с 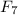F_7 по модулю 1000. Т.к последовательность возрастающая и неограниченная, начиная со 2ого члена, это утверждение эквивалентно условию задачи.

Доказано.

________________________________

Можно доказать аналогичным образом и более общее утверждение: последовательность чисел Фибоначчи по модулю 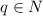$q\in N$ периодическая (вышеприведенные рассуждения - частный случай этого док-ва). Длина периода такой последовательности обозначается 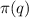$\pi(q)$ и называется период Пизано.