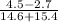
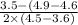
Пошаговое объяснение:
[ sin( π/2 + 3α)]/[ 1 - sin( 3α - π )] = ctg( 5π/4 + 3α/2 ) .
Перетворюємо окремо обидві частини рівності :
[ sin( π/2 + 3α)]/[ 1 - sin( 3α - π )] = cos3α/[ 1 +sin( π - 3α)] = cos3α/( 1 + sin3α ) ;
ctg( 5π/4 + 3α/2 ) = ctg( π + π/4 + 3α/2) = ctg(π/4 + 3α/2 ) =
= cos(π/4 + 3α/2 )/sin(π/4 + 3α/2 ) = cos( π + 6α)/4 : sin( π + 6α)/4 =
= √{ ( [1 + cos(π + 6α)/2 ]/2 } /√{ ( [1 - cos(π + 6α)/2 ]/2 } =
= √ [1 + cos(π + 6α)/2 ]/√ [1 - cos(π + 6α)/2 ] = √[ 1 + cos(π/2 + 3α)]/√[ 1 -
- cos( π/2 + 3α)] = √ ( 1 - sin3α) /√ ( 1 +sin3α) = √( 1-sin²3α) /√ ( 1 +sin3α)² =
= √cos²3α /√ ( 1 +sin3α)² = | cos3α/sin( 1 + 3α ) | = cos3α/sin( 1 + 3α ) .
Ліва частина дорівнює правій , тому дана рівність є тотожністю .
Ще треба обг'рунтувати , що в ОДЗ обидві частини рівності мають
однакові знаки .
Испытание состоит в том, что из 20 вопросов выбирают 8.
n=C⁸₂₀=20!/((20-8)!·8!)=13·14·15·16·17·18·19·20/(2·3·4·5·6·7·8)=13·17·3·19·10=
=
Пусть событие А - " из восьми вопросов знает ответ на 5, не знает на три"
Событию А благоприятствуют исходы:
m=C⁵₁₄·C³₆ - пять вопросов из четырнадцати выученных и три вопроса из шести невыученных
m= (14!/(14-5)!·5!)· (6!/(6-3)!·3!)= ((10·11·12·13·14)/(2·3·4·5)) · (4·5·6/(2·3))=
=11·13·14·4·5
По формуле классической вероятности
p(A)=m/n=(11·13·14·4·5)/(13·17·3·19·10)=(11·14·2)/(17·3·19)=308/969