2) коля поехал на дачу в велосипеде. сначала он ехал полчаса со скоростью 8км/ч. затем 18минут чинили велосипед. оставшиеся 8км пути он ехал со скоростью 10км/ч. с какой скоростью коля преодолел расстояние до дачи? ПОШАГОВОЕ РЕШЕНИЕ
полчаса -это 0,5 часа, поэтому Коля проехал первую часть пути: 0,5×8=4км
8÷10=0,8часа - время за которое Коля проехал оставшуюся часть пути и все расстояние, которое он проехал составило 4+8=12км
Если взять время, которое Коля потратил на дорогу без остановки, то он потратил 0,5+0,8=1,3 часа, тогда его чистая скорость была:
12÷1,3=12÷=12÷=12×= км/ч
18минут= часа, поскольку 1 час=60 минут и 18÷60=0,3
Учитывая время, которое он простоял, когда чинил велосипед, тогда он потратил времени: 1,3+0,3=1,6 часа потратил всего, тогда в этом случае его скорость составила 12÷1,6=7,5 км/ч
Функция, получающая бесконечно малые приращения прибесконечно малых приращениях аргумента. Однозначная функция f (x) называется непрерывной призначении аргумента x0, если для всех значений аргумента х, отличающихся достаточно мало от x0, значенияфункции f (x) отличаются сколь угодно мало от её значения f (x0). Точнее, функция f (х) называетсянепрерывной при значении аргумента x0 (или, как говорят, в точке x0), если каково бы ни было ε > 0, можноуказать такое δ > 0, что при |х — х0| < δ будет выполняться неравенство |f (x) — f (x0)| < ε. Это определениеравносильно следующему: функция f (x) непрерывна в точке x0, если при х, стремящемся к x0, значениефункции f (x) стремится к пределу f (x0). Если все условия, указанные в определении Н. ф., выполняютсятолько при х ≥ х0 или только при х ≤ х0, то функция называется, соответственно, непрерывной справа илислева в точке x0. Функция f (x) называется непрерывной н а отрезке [а, b], если она непрерывна в каждойточке х при а < х < b и, кроме того, в точке а непрерывна справа, а в точке b — слева. Понятию Н. ф. противопоставляется понятие разрывной функции (См. Разрывные функции). Одна и таже функция может быть непрерывной для одних и разрывной для других значений аргумента. Так, дробнаячасть числа х [её принято обозначать через (х)], например
Функция, получающая бесконечно малые приращения прибесконечно малых приращениях аргумента. Однозначная функция f (x) называется непрерывной призначении аргумента x0, если для всех значений аргумента х, отличающихся достаточно мало от x0, значенияфункции f (x) отличаются сколь угодно мало от её значения f (x0). Точнее, функция f (х) называетсянепрерывной при значении аргумента x0 (или, как говорят, в точке x0), если каково бы ни было ε > 0, можноуказать такое δ > 0, что при |х — х0| < δ будет выполняться неравенство |f (x) — f (x0)| < ε. Это определениеравносильно следующему: функция f (x) непрерывна в точке x0, если при х, стремящемся к x0, значениефункции f (x) стремится к пределу f (x0). Если все условия, указанные в определении Н. ф., выполняютсятолько при х ≥ х0 или только при х ≤ х0, то функция называется, соответственно, непрерывной справа илислева в точке x0. Функция f (x) называется непрерывной н а отрезке [а, b], если она непрерывна в каждойточке х при а < х < b и, кроме того, в точке а непрерывна справа, а в точке b — слева. Понятию Н. ф. противопоставляется понятие разрывной функции (См. Разрывные функции). Одна и таже функция может быть непрерывной для одних и разрывной для других значений аргумента. Так, дробнаячасть числа х [её принято обозначать через (х)], например
Пошаговое объяснение:
полчаса -это 0,5 часа, поэтому Коля проехал первую часть пути: 0,5×8=4км
8÷10=0,8часа - время за которое Коля проехал оставшуюся часть пути и все расстояние, которое он проехал составило 4+8=12км
Если взять время, которое Коля потратил на дорогу без остановки, то он потратил 0,5+0,8=1,3 часа, тогда его чистая скорость была:
12÷1,3=12÷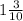 =12÷
=12÷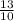 =12×
=12×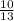 =
=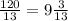 км/ч
км/ч
18минут=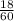 часа, поскольку 1 час=60 минут и 18÷60=0,3
часа, поскольку 1 час=60 минут и 18÷60=0,3
Учитывая время, которое он простоял, когда чинил велосипед, тогда он потратил времени: 1,3+0,3=1,6 часа потратил всего, тогда в этом случае его скорость составила 12÷1,6=7,5 км/ч