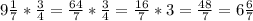
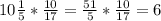
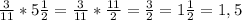
Числа геометричної прогресії - це 24, 72, 216, а числа арифметичної прогресії - це -24, 24, 72.
Пошаговое объяснение:
Позначимо перше число геометричної прогресії через a, а знаменник - через q. Тоді друге число буде a*q, а третє - a*q^2.
За умовою задачі маємо:
a + a*q + a*q^2 = 93 (1)
Також за умовою задачі маємо:
(a-48) + a*q + a*q^2 = 2a - 48 + a*q = a + (a*q - 48) + a*q^2
Отже, числа утворюють арифметичну прогресію з різницею d = a*q - 48.
Запишемо рівняння для різниці:
a*q - 48 = (a*q^2 - a*q) / 2
Розв'язавши його відносно a, отримаємо:
a = 96 / (3*q - 2) (2)
Підставимо (2) в (1) і спростимо:
96 / (3*q - 2) + 96*q / (3*q - 2) + 96*q^2 / (3*q - 2) = 93
Перенесемо все на одну сторону:
96 + 96*q + 96*q^2 - 93*(3*q - 2) = 0
Розв'язавши квадратне рівняння відносно q, отримаємо два корені:
q1 = -1/3
q2 = 3
Підставимо q1 в (2) і отримаємо a1 = -144. Це не може бути правильним розв'язком, тому візьмемо q2.
Підставимо q2 в (2) і отримаємо a2 = 24.
Отже, числа геометричної прогресії - це 24, 72, 216, а числа арифметичної прогресії - це -24, 24, 72.
Найдем наибольший общий делитель чисел 189 и 168:
$$
\begin{aligned}
189 &= 1 \cdot 168 +21 \\
168 &= 8 \cdot 21 +0 \\
\end{aligned}
$$
Значит, $\text{НОД}(189,168) =21$. Это означает, что максимальное количество наборов подарков будет равно количеству делителей числа $21^2$, так как каждый набор должен содержать одинаковое число пряников (которое является делителем числа $189$) и одинаковое число шоколадок (которое является делителем числа $168$).
Число $21^2=441$ имеет следующие делители: $$1,\;3,\;7,\;9,\;21,\;27,\;\textbf{49},\;\textbf{63},\;\textbf{147},\;\textbf{441}.$$ Здесь жирным выделены те делители, которые могут быть количеством наборов подарков. ответ: наибольшее количество таких наборов - $\boxed {4}$ (можно сделать четыре набора по $49$ пряникам и $49$ шоколадок в каждом).