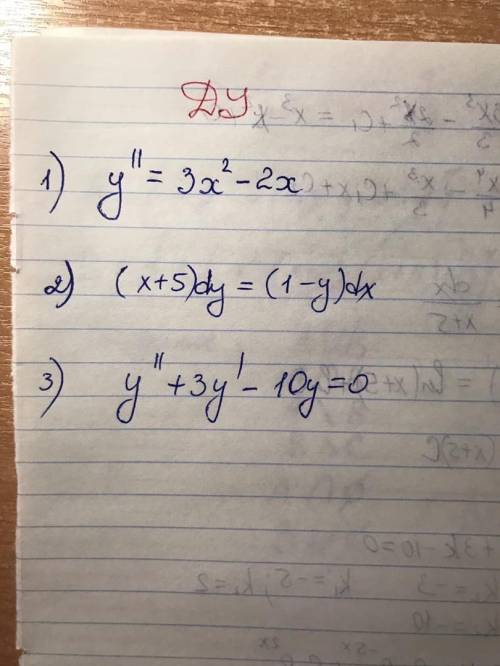
28/67 * (a - 2 11/13 : b) : c
при а = 10 11/13, b = 1/2, с = 3 1/2
28/67 * (10 11/13 - 2 11/13 : 1/2) : 3 1/2 = 8/13
1) 2 11/13 : 1/2 = 37/13 * 2 = 74/13 = 5 9/13
2) 10 11/13 - 5 9/13 = 5 2/13
3) 28/67 * 5 2/13 = 28/67 * 67/13 = 28/13
4) 28/13 : 3 1/2 = 28/13 : 7/2 = 28/13 * 2/7 = 8/13
(12 : а + b) : 1 1/2 - с
при а = 3 3/5, b = 2/3, с = 1 1/3
(12 : 3 3/5 + 2/3) : 1 1/2 - 1 1/3 = 1 1/3
1) 12 : 3 3/5 = 12 : 18/5 = 12 * 5/18 = 60/18 = 30/9 = 10/3
2) 10/3 + 2/3 = 12/3 = 4
3) 4 : 1 1/2 = 4 : 3/2 = 4 * 2/3 = 8/3
4) 8/3 - 1 1/3 = 8/3 - 4/3 = 4/3 = 1 1/3
Такой тип задач решается довольно просто. Представь, что парабола -- это какое-либо квадратное уравнение. В первом случае y=0.5x²+2x-1.
Точка пересечения с осью Оy означает, что x в данной точке равен нулю (Представь себе перекрестие осей x и y. Вертикальная прямая -- ось y. Если ты будешь беспорядочно проводить прямые, с осью y они будут пересекаться всегда в одной точке: в точке, где x=0). Значит, просто решаем уравнение с учётом, что x=0. y=0.5*0²+2*0-1
y = -1 (Точка пересечения с Оy) Записываем это в виде точки. Я назвала её как A.
A(0 ; -1)
Ситуация с точкой пересечения с Оx почти такая же, как с Оy, но наоборот. В это случае мы y приравниваем к нулю и снова решаем уравнение. 0= -x²-4x-3. (Предполагаю, у тебя допущена опечатка, раз тема парабола, так что я взяла x в квадрат).
x = -1;-3
Значит, с осью Ox парабола пересекается в двух местах. Назову эти точки B и C.
B(-3;0)
C(-1;0)
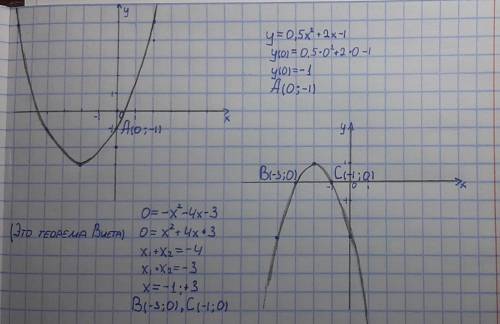
ответ: 1) y=1/4*x⁴-1/3*x³+C1*x+C2, где С1 и С2 - произвольные постоянные.
2) y=(x+5+C)/(x+5), где С≠0.
3) y=C1*e^(2*x)+C2*e^(-5*x), где С1 и С2 - произвольные постоянные.
Пошаговое объяснение:
1) y'=∫(3*x²-2*x)*dx=3*∫x²*dx-2*∫x*dx=x³-x²+C1; y=∫y'*dx=∫x³*dx-∫x²*dx+C1*∫dx=1/4*x⁴-1/3*x³+C1*x+C2, где С1 и С2 - произвольные постоянные.
2) Разделив уравнение на произведение (x+5)*(1-y), получаем уравнение dy/(1-y)=dx/(x+5), или dy/(y-1)+dx/(x+5)=0, или d(y-1)/(y-1)+d(x+5)/(x+5)=0. Интегрируя, находим ln/y-1/+ln/x+5/=ln/C/, или (y-1)*(x+5)=C, где C - произвольная, но не равная нулю, постоянная. Отсюда y-1=C/(x+5) и y=(x+5+C)/(x+5).
3) Перед нами - однородное ЛДУ 2 порядка с постоянными коэффициентами. Для его решения составляем характеристическое уравнение: k²+3*k-10=0. Оно имеет действительные и притом различные корни k1=2 и k2=-5, поэтому y=C1*e^(2*x)+C2*e^(-5*x), где С1 и С2 - произвольные постоянные.