
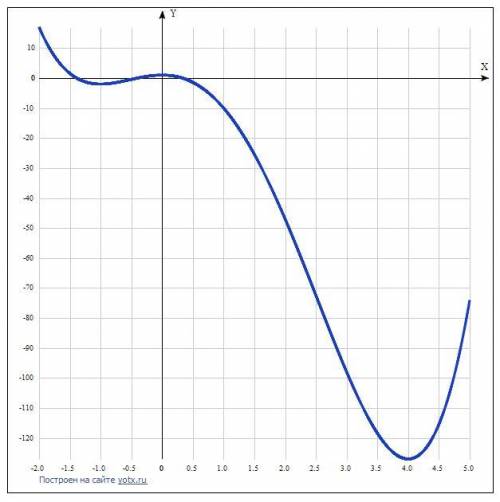
Дана функция у=x^4 -4x^3 -8x^2 +1.
Её производная равна 4x^3 - 12x^2 - 16x.
Приравняем производную нулю:
4x^3 - 12x^2 - 16x = 4x(x^2 - 3x - 4) = 0.
Первый множитель даёт корень х = 0.
Далее: x^2 - 3x - 4 = 0. Д = 9 + 16 = 25. х1 = (3-5)/2 = -1, х2 = (3 + 5)/2 = 4.
Находим знаки производной на промежутках.
х = -2 -1 -0,5 0 2 4 5
y' = -48 0 4,5 0 -48 0 120 .
Имеем экстремумы:
два минимума в точках х = -1 и х = 4 и один максимум в точке х = 0.
Значения функции в точках экстремумов:
х = -1, у = -2.
х = 0, у = 1,
х = 4, у = -127.
Пусть х - конфеты Белочка, тогда (62 - х) - конфеты красная Шапочка.
Уравнение: 1/4 * х = 4/15 * (62 - х)
1/4х = 248/15 - 4/15х
1/4х + 4/15х = 248/15
15/60х + 16/60х = 248/15
31/60х = 248/15
х = 248/15 : 31/60 = 248/15 * 60/31 = (8*4)/(1*1) = 32
х = 32 (шт.) - конфеты Белочка
62 - 32 = 30 (шт.) - конфеты Красная Шапочка
ответ: 32 Белочки и 30 Красных Шапочек.