3) При возведении обеих частей уравнения в одинаковую четную степень не всегда получаются равносильные уравнения.
Пошаговое объяснение:
1) Утверждение не верно.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня. Например:
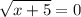
Это уравнение имеет корень х = -5!
2) Утверждение не верно.
Например, если возвести в нулевой степень (0 принадлежит множеству действительных чисел) уравнение, имеющий только корень х=0:
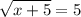
то получим
1 ≡ 1, что означает, последнее верно для любого х∈R.
3) Утверждение верно.
Уравнения называются равносильными, если имеют одно и то же множество корней.
В самом деле, рассмотрим иррациональное уравнение, которое не имеет корней:
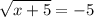
После возведения в квадрат получим:
x+5=25
А это уравнение имеет корень x=20!
Допустим, что число - бесконечная периодическая дробь. Тогда, начиная с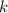
-ой цифры, некоторая последовательность из 
цифр будет повторяться бесконечно. Очевидно, что, после 
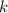-ой цифры найдутся ненулевые цифры. А значит искомый период длины 
содержит хотя бы одну ненулевую цифру.
Также очевидно, что в десятичной записи присутствует число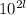
. В нем одна 1, а за ней следуют 
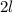нулей.
Пусть в период входят одна 1 и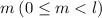
нулей этого числа. Но следующие 
цифр - нули (т.к. в предыдущее повторение периода вошло меньше, чем 
нулей, незадействованными остались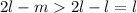 
подряд идущих нулей) - противоречие с тем, что в периоде есть ненулевая цифра.
А значит у дроби нет периода.
Т.к. она бесконечная (число натуральных чисел бесконечно), то иррациональная.
ответ: число иррационально