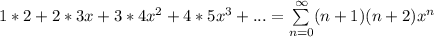
Это степенной ряд, найдём его радиус сходимости.
Согласно признаку Даламбера.
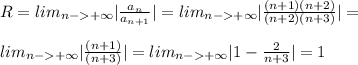
Так как радиус сходимости степенного ряда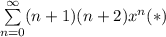 
равен 1, то при |x| >1, ряд расходится.
Проверим сходимость в точках x = 1 и x = -1.
При x = 1, ряд (*) — расходится (так как не выполняется необходимое условие сходимости числового ряда).
При x = -1, ряд (*) – расходится (так как не выполняется необходимое условие сходимости числового ряда).
Ряд сходится при |x| < 1.
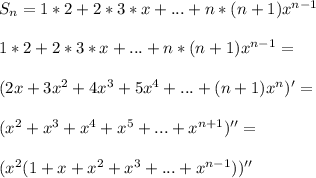
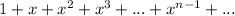- разложение в ряд Маклорена функции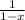 
См. дальнейшее решение во вложении.
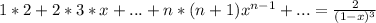при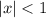 
2у-х=4 => 2y=4+x (при переносе через знак равенства какого-либо слагаемого, его знак должен изменитья на противоположный)
2y=4+x => y=(4+x)/2 ( чтобы избавиться от множителя в одной стороне уравнения, мы имеем право поделить другую сторону на то же число)
Вот и получился ответ, в котором "у" выражен через "х".
Для обратного результата - преобразуй так, чтобы "х" оказался в одиночестве в одной стороне уравнения:
2y-x=4 => 2y=4+x => 2y-4=x