Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .
Находим векторы АВ, АС и АД.
Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.
Вектор АC={xC-xA, yC-yA, zC-zA} = (-6; 3; -4) =√61 ≈ 7,81025.
Вектор АD={xD-xA, yD-yA, zD-zA} = (-6; -1; -2) = √41 ≈ 6,40312.
Определяем векторное произведение АВ х АС.
i j k | I j
-4 2 -1 | -4 2
-6 3 -4 | -6 3 = -8i + 6j - 12k - 16j + 3i + 12k = -5i - 10j = (-5; -10; 0).
Далее находим смешанное произведение (АВ х АС) х АД.
(АВ х АС) = (-5; -10; 0),
АD = (-6; -1; -2),
(АВ х АС) х АД = 30 + 10 + 0 = 40.
Объем пирамиды равен (1/6) этого произведения:
V = (1/6)*40 = (20/3) куб.ед.
Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).
Площадь основания АВС равна половине модуля векторного произведения АВ х АС.
S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.
h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.
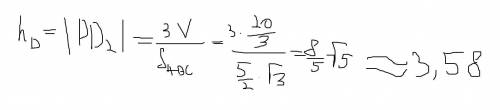
6 : 2 = 3 9 : 3 = 3 10 : 2 = 5
3 : 3 = 1 3 : 3 = 1 5 : 5 = 1
6 = 2 * 3 9 = 3 * 3 10 = 2 * 5
НОК (6; 9; 10) = 2 * 3 * 3 * 5 = 90 - наименьшее общее кратное
Чтобы найти НОК (a; b), нужно разложить данные числа на простые множители и найти произведение всех простых множителей, взятых с наибольшим показателем степени.
Любое число, кратное 90 (НОК чисел 6; 9; 10), будет общим кратным для этих чисел. Например:
90 * 2 = 180 90 * 3 = 270 90 * 4 = 360 90 * 5 = 450 и т.д.
180 : 6 = 30 270 : 6 = 45 360 : 6 = 60 450 : 6 = 75
180 : 9 = 20 270 : 9 = 30 360 : 9 = 40 450 : 9 = 50
180 : 10 = 18 270 : 10 = 27 360 : 10 = 36 450 : 10 = 45
216 см площа куба
сторона куба 6 см
Пошаговое объяснение: