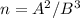, такие что
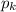- неповторяющиеся простые числа. Построим числа A и B по следующему алгоритму. Примем сначала A=B=1. Для каждого k-го множителя в разложении числа n есть два варианта.
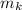четная, домножим число A на 
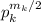. Тогда числитель A^2 будет содержать множитель 
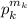, а так как знаменатель B^3 не содержит такого множителя, частное будет тоже содержать множитель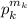 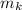нечетная, домножим A на 
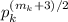, а B домножим на 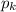. Тогда легко видеть, что отношение A^2 к B^3 будет содержать 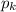в степени 
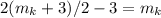, что нам и надо
Всего 10х пуговиц.
Это число не делится на целом на 9 или на 6. Поэтому это не 30, не 60 и не 90.
Возможные варианты 10,20,40,50,70,80,100.
10:9=1 и 1 в остатке. 10:6=1 и 4 в остатке - подходит.
20:9=2 и 2 в остатке. 20:6=3 и 2 в остатке - не подходит.
40:9=4 и 4 в остатке. 40:6=6 и 4 в остатке - не подходит.
50:9=5 и 5 в остатке. 50:6=8 и 2 в остатке - не подходит.
70:9=7 и 7 в остатке. 70:6=11 и 4 в остатке - не подходит.
80:9=8 и 8 в остатке. 80:6=13 и 2 в остатке - не подходит.
100:9=11 и 1 в остатке. 100:6=16 и 4 в остатке - подходит.
Если исходить из того, что "несколько наборов" означает два и более наборов, то ответ 100 пуговиц.
Если несколько наборов" означает один и более наборов, то два ответа: 10 и 100 пуговиц.
Кроме того, числа от 40 по 80 можно было не проверять, так как остаток от деления на 6 всегда меньше, чем 6. Поэтому остаток от деления на 9 дожен быть меньше, чем 3.