Квадрат - это четырехугольник, у которого все стороны равны, все углы равны (все углы прямые).
1) Зная периметр квадрата, найдем его сторону (a):
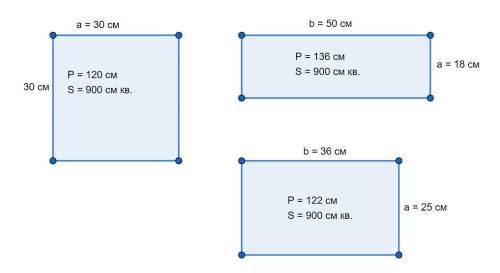
P(кв) = 4a = 120 см. a = 120/4 = 30 см.
Найдем площадь квадрата со стороной 30 см.
S кв = a*a = 30 см *30 см = 900 см кв.
2) Площадь прямоугольника равна произведению длины (a) на ширину (b).
S пр = a * b = 900 см кв.
а) Это может быть прямоугольник со сторонами 18 см и 50 см.
Его площадь равна площади заданного квадрата:
S₁ = 18 см * 50 см = 900 см кв.
Найдем периметр этого прямоугольника
P₁ = 2(a+b)=2(18 см + 50 см) = 2 * 68 см = 136 см.
Периметр квадрата меньше периметра прямоугольника. P < P₁
б) Прямоугольник со сторонами 25 см и 36 см. Его площадь также равна площади квадрата:
S₂ = 25 см * 36 см = 900 см кв.
Найдем периметр второго прямоугольника:
P₂ = 2(a+b)=2(25 см +36 см) = 2 * 61 см = 122 см.
Периметр квадрата меньше периметра прямоугольника. P < P₂.
Вывод. Периметр квадрата меньше периметра прямоугольника той же площади.
(a²√5)/2
Пошаговое объяснение:
Так как K середина, то DK=KD₁
Раз сечение проходит через точки A и B, то сторона AB находится на этой плоскости, также плоскость делит ребро СС₁ на точке M, которая середина для нее CM=MC₁ так как KM║DC║D₁C₁
Отсюда следует что KM=a и KD=MC=a/2
Из прямоугольника ΔADK следует что AD²+KD²=AK²
AK²=a²+a²/4 ⇒AK²=5a²/4 ⇒ AK=(a√5)/2
Так как сторона BA перпендикулярно плоскости AA₁D₁D то оно перпендикулярно любих линии проходящей через тичку A и находящиеся на плоскость AA₁D₁D․ Отсюда получаем что AB⊥AK
Получается что AKMB является прямоугольником и площадь его AK*AB=a*(a√5)/2=(a²√5)/2