1)Да. Четыри прямых, две из которых проходят через диагонали квадрата, а другие две через середины противоположных сторон. Ето легко показать если взять квадратный лист бумаги и сложить пополам и розложыть - тогда линия сгина и будет частю (сгин конечен, а прямая - нет) оси симетрии. А таких разных складываний есть 4. 2)Нет. Треугол. бывают с прямым углом - прямоуголные. есть такая теорема:сума углов треугольника равна 180 гр., а так как 90 менше 180, то на остальные 2 угла остается еще 90 гр. то есть существуют треугольники с углом 90гр. 3)Да. Пускай m:n=m*(1/n) операцию деления поменяем умножением. Уменшим делимое и повтори замену операций (m:2):n=(m*1/2)*1/n=. А теперь скобки можна опустить так как неважно в каком порядке перемножать - результат тот же. =m*1/n*1/2, а m*1/n есть частное которое умн. на 1/2 и будет в два раза менше. Например: 12:3=4. 12:2:3=2 4)Нет. Пускай сторона квадрата 2а, тогда его площа S=(2a)^2=4a^2. Уменшим сторону в двое- получим квадрат с стороной а и площей S1=a^2 и видим что его площа в 4 раза менше, а не в два.
1) Вычеркнули все нечетные числа. Остались 2,4,6,8,10,12,14,,2008. То есть числа, кратные 2. 2) Разделим каждое из чисел на 2 и получим ряд 1,2,3,1004. Вычеркнем среди них числа на нечетных местах, то есть нечетные числа. Останется 2,4,,1004. Снова получили числа, кратные 2. И это с учетом того, что их уже до этого делили на 2. Это значит, что на втором шаге остались только кратные 4=2^2. Продолжим делать подобное и заметим, что на k-м шаге останутся только числа, кратные 2^k. На 10-м шаге останется лишь число 1024, все остальные будут вычеркнуты. ответ: 1024.
Так как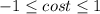
, то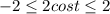 
.
А значит,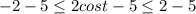
, то есть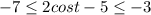 
Таким образом, наименьшее значение равно -7.