Даны вершины треугольника: А(-2; -1), B(1; 4), C(2; -3).
Выполнить:
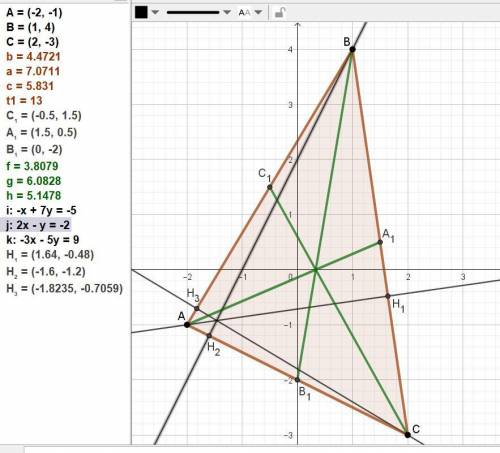
1. Постройте ∆АВС по координатам. Проведите медианы АА1, BB1, CC1. Постройте высоты AH1, ВН2, СН3.
Даны на прилагаемом рисунке.
2. Запишите уравнения сторон AB, BC, AC.
Находим векторы.
Вектор АВ = (1-(-2); 4 -(-1)) = (3; 5). Модуль равен √(3² + 5²) = √34.
Вектор ВС = (2-1; -3 -4) = (1; -7). Модуль равен √(1² + (-7)²) = √50.
Вектор АС = (2-(-2); -3 -(-1)) = (4; -2). Модуль равен √(4² + (-2)²) = √20 = 2√5.
Определяем уравнения сторон.
AB: (x + 2)/3 = (y + 1)/5 каноническое,
5x – 3y + 7 = 0 общее,
y = (5/3)x + (7/3) с угловым коэффициентом.
ВС: (x - 1)/1 = (y - 4)/(-7) каноническое,
7x + y - 11 = 0 общее,
y = -7x + 11 с угловым коэффициентом.
АС: (x + 2)/4 = (y + 1)/(-2) каноническое,
2x + 4y + 8 = 0 или x + 2y + 4 = 0 общее,
y = (-1/2)x - 2 с угловым коэффициентом.
3. Найдите длины сторон треугольника АВС. Определите вид треугольника по сторонам (равносторонний, разносторонний, равнобедренный).
Длины (модули) сторон найдены в п.2).
Вид треугольника по сторонам: разносторонний.
4. Найдите углы ∆АВС. Определите вид треугольника по углам (прямоугольный, остроугольный, тупоугольный).
Углы по теореме косинусов
cos A = (b^2+c^2-a^2)/(2bc) 4 52,1536192 0,0767
A = arccos 0,0767 = 1,494024 радиан 85,6013 градуса
cos B = (a^2+c^2-b^2)/(2ac) 64 82,4621125 0,77611
B = arccos 0,77611 = 0,682317 радиан 39,0939 градуса
cos C = (a^2+b^2-c^2)/(2ab) 36 63,2455532 0,56921
C = arccos 0,56921 = 0,965252 радиан 55,3048 градуса
Вид треугольника по углам: остроугольный.
5. Найдите длины медиан АА1, ВВ1, СC1. А(-2; -1), B(1; 4), C(2; -3).
Находим координаты точки А1 как середины стороны ВС.
А1 = (B(1; 4) + C(2; -3)) / 2 = (1,5; 0,5).
Вектор АА1 = (1,5-(-2); 0,5-(-1)) = (3,5; 1,5)
Уравнение АА1: (х + 2)/3,5 = (у + 1)/1,5,
или в целых числах (х + 2)/7 = (у + 1)/3.
Находим координаты точки В1 как середины стороны АС.
В1 = (А(-2; -1) + C(2; -3))/2 = (0; -2).
Вектор ВВ1 = (0 -1; -2-4) = (-1; -6).
Уравнение ВВ1: (х - 1)/(-1) = (у -4)/(-6).
Находим координаты точки С1 как середины стороны АВ.
С1 = (А(-2; -1) + B(1; 4)) / 2 = (-0,5; 1,5).
Вектор СС1 = (-0,5-2); 1,5-(-3)) = (-2,5; 4,5),
Уравнение СС1: (х - 2)/(-2,5) = (у + 3)/4,5.
или в целых числах (х - 2)/(-5) = (у + 3)/9.
Длины медиан X Y Модуль
АА1= √(3,5² + 1,5²) = 3,8079,
ВВ1= √((-1)² + (-6)²) = 6,0828,
СС1= √((-2,5)² + 4,5²) = 5,1478.
6. Найдите длины высот AH1, ВН2, СН3.
Высота АН1 перпендикулярна стороне ВС: 7x + y - 11 = 0.
Её уравнение имеет вид х - 7у + С = 0 (коэффициенты А и В из уравнение стороны АВ меняются на В и -А).
Для определения величины С подставим координаты точки А(-2; -1).
АН1: 1*(-2) - 7*(-1) + С = 0, отсюда С = 2 - 7 = -5.
АН1: х - 7у - 5 = 0.
Длина высоты AH1 – это расстояние от точки А до противолежащей стороны ВС.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C|
√(A² + B²)
Подставим в формулу данные: ВС: 7x + y - 11 = 0, А(-2; -1).
d = |7·(-2) + 1·(-1) - 11| |-14 - 1 - 11|
√(7² + 1²) = √(49 + 1) =
= 26/√50 = 26√2/10 ≈ 3,677.
Высота ВН2 перпендикулярна стороне АС: x + 2y + 4 = 0.
Её уравнение имеет вид 2х - у + С = 0 (коэффициенты А и В из уравнения стороны АC меняются на В и -А).
Для определения величины С подставим координаты точки B(1; 4).
ВН2: 2*1 - 1*4 + С = 0, отсюда С = -2 + 4 = 2.
ВН2: 2х - у + 2 = 0.
Длина высоты ВH2 – это расстояние от точки В до противолежащей стороны АС.
Подставим в формулу данные: АС: x + 2y + 4 = 0, B(1; 4).
d = |1·1 + 2·4 + 4| |1 + 8 + 4|
√(1² + 2²) = √(1 + 4) =
= 13/√5 = 13√5/5 ≈ 5,814.
Высота СН3 перпендикулярна стороне АВ: 5x – 3y + 7 = 0.
Её уравнение имеет вид 3х + 5у + С = 0 (коэффициенты А и В из уравнение стороны АВ меняются на -В и А).
Для определения величины С подставим координаты точки С(2; -3).
СН3: 3*2 + 5*(-3) + С = 0, отсюда С = -6 + 15 = 9.
СН3: 3х + 5у + 9 = 0.
Длина высоты CH3 – это расстояние от точки С до противолежащей стороны AB.
Подставим в формулу данные: АВ: 5x – 3y + 7 = 0, С(2; -3).
d = |5·2 - 3·(-3) + 7| |10 + 9 + 7|
√(5² + (-3)²) = √(25 + 9) =
= 26/√34 = 13√34/17 ≈ 4,459.
В решении.
Пошаговое объяснение:
а)
1) Возвести значение х в квадрат; (2/7)² = 4/49;
2) Умножить итог возведения в степень на 0,49; 4/49 * 0,49 = 0,04;
3) Возвести у в третью степень; (0,1)³ = 0,001;
4) Умножить итог возведения на 430; 0,001 * 430 = 0,43;
5) Сложить итоги умножений; 0,04 + 0,43 = 0,47;
б)
1) Возвести значение х в третью степень; (-2/3)³ = -8/27;
2) Разделить 168 на итог возведения; 168 : (-8/27) = -(168*27)/8 = -567;
3) Возвести у в квадрат; (-0,5)² = 0,25;
4) Разделить 150 на итог возведения; 150 : 0,25 = 600;
5) Из первого частного вычесть второе частное; -567 - 600 = -1167;
в)
1) Возвести х в четвёртую степень; 2⁴ = 16;
2) Возвести 3 в третью степень; 3³ = 27;
3) Перемножить итоги возведения в степень; 16 * 27 = 432;
4) Разделить произведение на 18; 432 : 18 = 24;
5) Возвести у в квадрат; 24² = 576;
6) Сложить частное и итог возведения в степень; 24 + 576 = 600;
г)
1) Возвести х в третью степень; (-0,4)³ = -0,064;
2) Возвести 0,5 в квадрат; 0,5² = 0,25;
3) Перемножить итоги возведения в степень; 0,25 * (-0,064) = -0,016;
4) Возвести (-0,5) в квадрат; (-0,5)² = 0,25;
5) Возвести у в третью степень; 0,4³ = 0,064;
6) Перемножить итоги возведения в степень; 0,25 * 0,064 = 0,016;
7) Сложить первое и второе произведения;
-0,016 + 0,016 = 0.