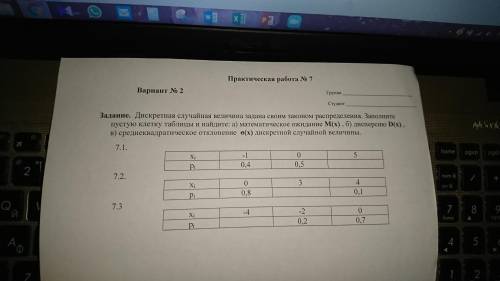
Делаю по формуле, на примере первого: х×1%/100%=3 тогда 3×100%/1%=300
1 стоблик:
3×100%/1%=300
6×100%/6%=100
7×100%/10%=70
21×100%/7%=300
36×100%/20%=180
70×100%/30%=200
80×100%/25%=320
1,2×100%/4%=30
6,5×100%/2%=325
35×100%/14%=250
Второй столбик:
45×100%/18=250
11×100%/55%=20
56×100%/28%=200
76×100%/19%=400
8,1×100%/27%=30
3,6×100%/15%=24
2,4×100%/80%=3
4×100%/16%=25
3,4×100%/17%=20
15×100%/3%=500
3,2×100%/16%=20
11×100%/22%=50
1,8×100%/30%=6
90×100%/45%=200
220×100%/55%=400
7×100%/56%=12,5
66×100%/33%=200
72×100%/12=600
/ Это деление
Пошаговое объяснение:
ответ:
пошаговое объяснение:
возьмем какую-либо вершину. просто выбрали любую. теперь "идем" по ребрам графа, не проходя по каждому ребру более 1 раза. поскольку циклов нет, рано или поздно мы "" в какую-нибудь вершину, у которой только 1 ребро, по которому мы в нее зашли. заметим, что тогда ее степень равна 1. возьмем и выкинем эту вершину и ее единственное ребро из графа. теперь кол-во вершин в графе - n-1, а ребер m-1 (m - кол-во ребер в изначальном графе). при этом связности мы не испортили, т.к. у нее было только одно ребро, которое мы выкинули с этой же вершиной!
проделаем ту же операцию. таким образом мы уменьшаем кол-во ребер и вершин каждым шагом на 1. рассмотрим граф, в котором осталось 2 вершины. одна из этих вершин имеет степень 1. значит и вторая тоже (при условии, что нет двойных ребер, но граф связен, поэтому их нет). уберем последнюю "единичную" вершину. у нас осталась одна вершина и ни одного ребра. а значит вершин изначально было на 1 больше, чем ребер. доказано.
p.s.: где достал(а)? какой город? )
подробнее - на -