Пошаговое объяснение:
Задача а)
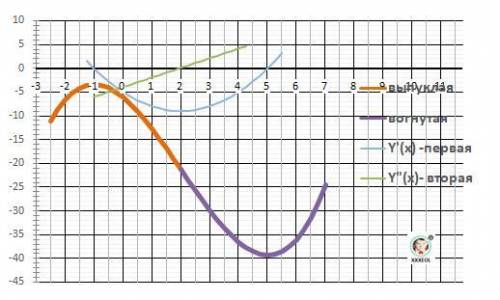
y = 1/3*x³ - 2*x² - 5*x - 6 - функция.
1) Область определения функции - ООФ - монотонность.
Непрерывная, гладкая.
D(x) = (-∞;+∞) - ответ.
2) Поиск экстремума по первой производной.
y'(x) = x² - 4*x - 5 = 0 - решаем квадратное уравнение
x1 = - 1, x2 = 5 - точки экстремумов.
3) Локальные экстремумы.
Ymin(5) = - 39 1/3, Ymax(-1) = - 3 1/3 - ответ.
Рисунок с графиком функции - в приложении.
Задача б)
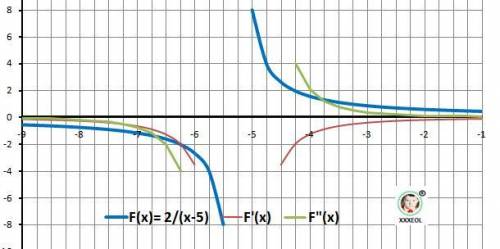
Дано: y = 2/(x-5).
(Текст решения с излишествами - полное исследование)
Исследование:
1. Область определения: D(y)= X≠ -5, X∈(-∞;-5)∪(-5;+∞). Не допускаем деления на 0 в знаменателе.
2.Поведение в точке разрыва. LimY(-5-)= -∞, LimY(-5+)= +∞. Вертикальная асимптота - х = -5.
Неустранимый разрыв II-го рода.
3. Поведение на бесконечности - наклонная асимптота.
k = lim(+∞)Y(х)/x = 2/(x²--5*х) = 0 - коэффициент наклона. y = 0 - горизонтальная асимптота.
4. Нули функции, пересечение с осью ОХ. Y(x) = 0 - нет.
5. Пересечение с осью ОУ. Y(0)= -2/-5 = 0,4
6. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;-5). Положительна: Y>0 - X∈(-5;+∞;)
7. Проверка на чётность. Есть сдвиг по оси ОХ - нет симметрии ни осевой ни центральной.
Функция общего вида - ни чётная, ни нечётная: Y(-x) ≠ -Y(x) , Y(-x)≠ Y(x).
8. Поиск экстремумов по первой производной.
y'(x) = - 2/(x-5)² = 0. Корней - нет.
9. Локальные максимумы - нет.
10. Интервалы монотонности.
Убывает: X∈(-∞;-5)∪(-5;+∞) - везде, где существует.
11. Поиск перегибов по второй производной.
y''(x) = 4/(x-5)³ = 0.
Точки перегиба нет, кроме точки разрыва при Х = 0.
12. Выпуклая - 'горка' - X∈(-∞;-5). Вогнутая - 'ложка'- X∈(-5;+∞;).
13. Область значений. E(y) - y∈(-∞;+∞).
14. График функции на рисунке в приложении.
по ровной V₁ --- 3 км/час
путь по ровной туда и обратно равный S₁;
в гору V₂ 2 км/час
с горы V₃ 6 км/час
и в гору и с горы равный S₂
общее время t ?час
Решение:
t = S/V
t₁ = S₁/V₁ = S₁/3 (час) время по ровной дороге туда и такое же обратно;
t₂ = S₂/V₂ = S₂/2 (час) время подъема в гору;
t₃ = S₂/V₃ = S₂/6 (час) время спуска с горы
t = (t₁ + t₂ + t₃ + t₂) (час) -- общее время складывается из времени прохода по ровной дороге, подъема, спуска и возвращения по ровной.
t = 2S₁/3 + S₂/2 + S₂/6 = 4S₁/6 + 3S₂/6 + S₂/6 = (4/6)(S₁ + S₂) = 4/6S общее время
S = S₁ + S₂ = 1, 5 км по условию
t = (4/6) * 1,5 = 1 (час)
ответ: Б. 60 мин. (или 1 час) продолжалась прогулка.