Пошаговое объяснение:
продифференцируем F(x)
F'(x) = 2/3 * 3x² - 4 * 2x + 6 = 2x² - 8x + 6 = f(x) => F(x) первообразная для f(x)
б) решим уравнение f(x) = 0
x² - 4x + 3 = 0
(x - 3)(x - 1) = 0
x₁ = 1; x₂ = 3 - экстремумы
F(-1) = -2/3 - 4 - 6 = -10 2/3 - наименьшее значение
F(1) = 2/3 - 4 + 6 = 2 2/3
F(3) = 18 - 36 + 18 = 0
F(4) = 128/3 - 64 + 24 = 2 2/3
г) F(x) = bx
2x³ - 12x² + 18x = 3bx
x(2x² - 12x + 18 - 3b) = 0
x₁ = 0 -первый корень
значит квадратный трехчлен должен иметь ровно один корень
для этого D = 0
D = 144 - 8(18 - 3b) = 0
18 - 3b = 144/8
18 - 3b = 18
3b = 0
b = 0
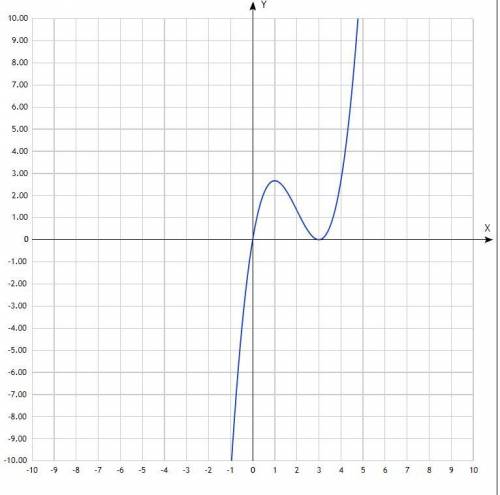
в) в приложении
Один пешеход шел из А в В - назовем его АВ
Второй шел из В в А - назоем его ВА.
АВ от А до места встречи затратил 40 мин, от места встречи до В -32 минуты.
Всего 72 минуты время пешехода АВ.
ВА до места встречи из В шел 40 мин, от места встречи до А - х минут, всего 40+х минут.
Каждый из них шел с разной скоростью.
Примем участок пути от места встречи до В, о котором известно время каждого, за у
Тогда скорость АВ равна у:32 км/мин
Скорость ВА равна у:40 км/мин
Оба пешехода равное расстояние от А до В и от В до А
Найдем для каждого это расстояние по формуле S=tv
Для АВ S=tv=72*у/32 км
Для ВА S=tv=(40+х)*у/40 км
Составим уравнение:
72*у/32=(40+х)*у/40
Умножим обе части уравнения на 32*40, чтобы избавиться от дробей:
72у*40=32у(40+х)
Сократим для облегчения вычислений обе части уравнения на 8*4 у, получим
9*10=40+х
х=50 ( мин)
ВА шел от места встречи до А 50 минут, а после своего выхода из В он пришел в А через 40+50=90 мин или 1,5 часа.