21 или 40
Пошаговое объяснение:
Зависит от того, могут ли повторяться цифры в числе.
ЕСЛИ ЦИФРЫ ЧИСЛА НЕ ПОВТОРЯЮТСЯ
Последней цифрой числа, кратного 5, могут быть только 0 или 5.
Если последняя цифра 0, то на каждое из оставшихся двух мест можно поставить любую из оставшихся четырех цифр. Для этого (по правилу умножения) существует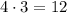 
вариантов выбора.
Если последняя цифра 5, то на первое место можно поставить любую из трех оставшихся цифр (кроме 0), а посередине — любую из оставшихся после предыдущего выбора цифр. В этом случае (по тому же правилу умножения) выходит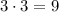 
вариантов.
Таким образом, для случая с неповторяющимися цифрами есть (по правилу сложения)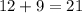 
вариант.
ЕСЛИ ЦИФРЫ ЧИСЛА ПОВТОРЯЮТСЯ
Для первого места есть четыре варианта выбора (кроме нуля), для последнего — два варианта (0 или 5), для среднего — все 5 цифр. По правилу умножения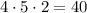 
вариантов.
вероятность того, что наугад взятый спортсмен выполнит квалификационную норму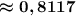
Пошаговое объяснение:
Уравнение полной вероятности.
Всего курсантов (15+10+5) = 30
Гипотезы и их вероятности (вероятности вычисляем по классическому определению вероятности P=m/n)
Н₁ = {выбран курсант 1 факультета}
P(H₁) = 15/30
Н₂ = {выбран курсант 2 факультета}
P(H₂) = 10/30
Н₃ = {выбран курсант 3 факультета}
P(H₃) = 5/30
Событие А = {наугад взятый спортсмен выполнит rвалификационную норму }
Условные вероятности нам даны в описании задачи
P(A|H₁) = 0,87
P(A|H₂) = 0,76
P(A|H₃) = 0,74
Формула полной вероятности
P(A) = P(H₁)*P(A|H₁) + P(H₂)*P(A|H₂) + P(H₃)*P(A|H₃)
Подставим наши данные
Таким образом, вероятность того, что наугад взятый спортсмен выполнит квалификационную норму ≈ 0,8117