Question

Обчислити інтеграли методом безпосереднього інтегрування:

Answer 1

$1)\int\limits \frac{3x - 5}{ \sqrt{6 {x}^{2} + 3 } } dx = \int\limits \frac{3xdx}{ \sqrt{16 {x}^{2} + 5} } - \int\limits \frac{5dx}{ \sqrt{16 {x}^{2} + 5 } } = \\ = \frac{3}{32} \int\limits \frac{32xdx}{ \sqrt{16 {x}^{2} + 5 } } - 5\int\limits \frac{dx}{ \sqrt{ {(4x)}^{2} + {( \sqrt{5}) }^{2} } } = \\ = \frac{3}{32} \int\limits \frac{d(16 {x}^{2} + 5)}{ {(16 {x}^{2} + 5) }^{ \frac{1}{2} } } - \frac{5}{4} \int\limits \frac{d(4x)}{ \sqrt{ {(4x)}^{2} + {( \sqrt{5}) }^{2} } } = \\ = \frac{3}{32} \frac{ {(16 {x}^{2} + 5) }^{ \frac{1}{2} } }{ \frac{1}{2} } - \frac{5}{4} \times \frac{1}{ \sqrt{5} } arctg( \frac{4x}{ \sqrt{5} } ) + C = \\ = \frac{3}{16} \sqrt{16 {x}^{2} + 5} - \frac{ \sqrt{5} }{4} arctg( \frac{4x}{ \sqrt{5} } ) + C$

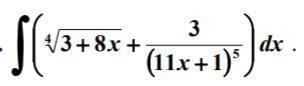
$2)\int\limits( \sqrt[4]{3 + 8x} + \frac{3}{ {(11x + 1)}^{5} } )dx = \\ = \frac{1}{8} \int\limits {(3 + 8x)}^{ \frac{1}{4} } d(3x + 8) + \frac{3}{11} \int\limits \frac{d(11x + 1)}{ {(11x + 1)}^{5} } = \\ = \frac{1}{8} \times \frac{ {(3 + 8x)}^{ \frac{5}{4} } }{ \frac{5}{4} } + \frac{3}{11} \times \frac{ {(11x + 1)}^{ - 4} }{( - 4)} + C = \\ = \frac{1}{10} \sqrt[4]{ {(8x + 3)}^{5} } - \frac{3}{44 {(11x + 1)}^{4} } + C$