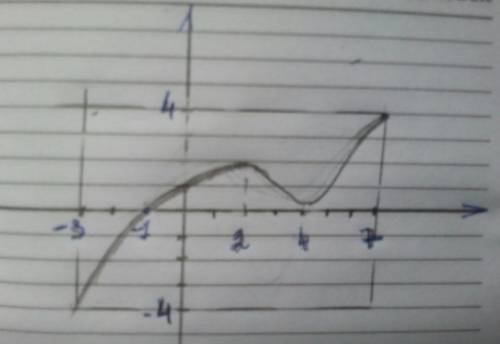
Пошаговое объяснение:
1) сначала строим оси координат
2) отмечаем промежутки ООФ [-3; 7] и ООП [-4; 4]
и строим прямоугольник - это тут мы будем строить график
3) отмечаем единственный нуль функции х = -1
4) отмечаем отрезки возрастания и убывания функции - наносим на ось Х точки 2 и 4
теперь можно и строить график. поскольку нам не даны точки минимума и максимума функции, то уж как нарисуем, так и будет. тем более, что в условии сказано не "построить" (т.е. точно воспроизвести) а "изобразить"
ну, в общем, что-то как на рисунке....
ответ:1)функция убывает; если х∈(-2;-1); функция возрастает, если х∈(-∞;-2)∪ (-1;+∞)
2) -π/2 + 2nπ, где n∈Z; (-1)ⁿ·arcsin(2/3) +nπ, где n∈Z
Пошаговое объяснение:1) у=2х³+9х²+12х-2, область определения D(y)=R, 2) y'= 6x²+18x+12 ⇒ y'=0, если 6x²+18x+12=0 ⇒ x²+3x+2 ⇒ дискриминант D=9-8=1, x₁=-1; х₂=-2 - критические точки; 3)критические точки x₁=-1; х₂=-2 разбивают область определения (всю координатную прямую ) на 3 интервала: (-∞;-2), (-2;-1) и (-1;+∞). Найдём знак производной на каждом из этих интервалов:
на (-∞;-2) у' (-3)=6·(-3)²+18·(-3)+12= 54-54+12 =12 >0
на (-2;-1) y'(-1,5)=6·(-1.5)²+18·(-1,5)+12=13,5-27+12=-1,5 <0
на (-1;+∞) y'(0)=12>0
Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает, значит:
функция убывает; если х∈(-2;-1); функция возрастает, если х∈(-∞;-2)∪ (-1;+∞)
2)3cos^2(x) - sinx - 1 = 0⇒ 3Сos²x-Sinx-1=0⇒3 (1- Sin²x)-Sinx-1=0 ⇒ 3 - 3 Sin²x-Sinx-1=0 ⇔ 3 Sin²x+Sinx-2=0; пусть Sinx=y, причём |y|≤1, тогда 3у²+у-2=0 ⇒ D=1+24=25>0 ⇒ y₁= (-1+5)/6=2/3, y₂=-1 ⇒
а)Если Sinx=-1, то х= -π/2 + 2nπ, где n∈Z;
б) Если Sinx=2/3, то х= (-1)ⁿ·arcsin(2/3) +nπ, где n∈Z
задание Напишите пять чисел кратных числу 7 это 14 , 21, 28, 35, 42 30 это 60, 90, 120, 150, 180 100 это 200, 300, 400, 500, 600 34 это 68, 102, 136, 170, 204 16 это 32 48 64 80 96 12 это 24 36 48 60 72 150 это 300 450 600 750 900 47 это 96 141 188 235 282
ДА ХОТЬ СТО