Павел Петрович, Александр Павлович, Николай Павлович, Александр Николаевич, Александр Александрович, Николай Александрович.
Пошаговое объяснение:
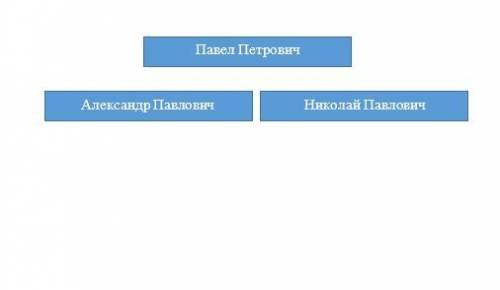
Павел Петрович не мог быть никому из них сыном или братом. У него одного только отчество Петрович. Значит он был первым. Тогда у него было два сына: Александр Павлович и Николай Павлович. См. рис.1
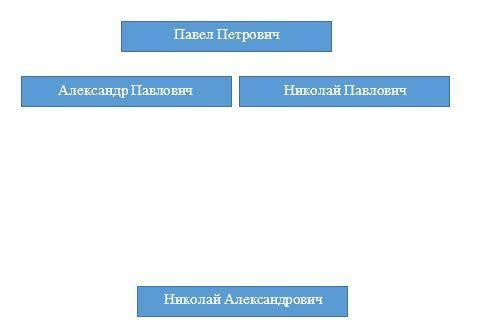
Последний был Николай. Николай Павлович, как выяснили, был или вторым, или третьим. Значит, последним был Николай Александрович. См. рис.2
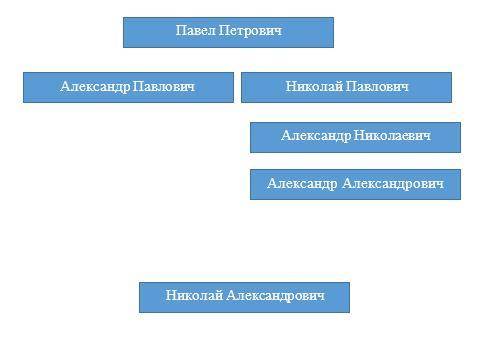
Осталось двое: Александр Александрович и Александр Николаевич. Если бы Александр Александрович был сыном Александр Павловича, то Александр Николаевич не мог бы быть его сыном. Значит, сын был у Николай Павловича. См. рис.3
Ну и поскольку сыновья следовали сразу за отцами, получаем окончательный порядок следования. См. рис.4

588
Пошаговое объяснение:
Карта дорог представляет собой три двудольных графа.
число дорог равно 3*14*14 = 588.
существует путь, проходящий через все дороги.
Действительно, каждый отдельно взятый двудольный граф с четным числом вершин в каждой дольке можно обойти по следующему алгоритму (здесь 1,2,3,4 - вершины первого графа, a,b,c,d - вершины второго графа):
1a2b1c2d1e2f1g2h1i2j1k2l1m2n...
...3a4b3c4d3e4f3g4h3i4j3k4l3m4n...
...
Алгоритм обхода всех дорог может быть таким:
1) обходим первый двудольный граф полностью;
2) обходим второй граф весь, кроме последней дороги;
3) обходим третий граф полностью;
4) проходим последнюю дорогу второго графа.
Вот відповідь