ответ: 1140
Объяснение:
в треугольнике 3 вершины. На первое место можно поставить 20 точек, на второе - 19, на третье - 18 => перемножив эти числа мы получим количество возможных треугольников. Но так мы посчитаем повторяющиеся треугольники, посему полученны результат нужно будет разделить на 3!=6
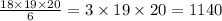
Используем одну из формул комбинаторики. Порядок размещения не учитывается, поэтому мы используем следующую формулу:
C - эс из n по k - k наверху как степень, n как k только снизу
С=n!/k!(n-k)!
n=20, k=3
С = 20!/3!(20-3)! = 20!/3!17! = 1140
{-R1*cos70+R2*cos45=0 {R1*cos70-R2*cos45 = 0 (меняем знаки)
{R1*cos20+R2*cos45-G=0 {R1*cos20+R2*cos45 = G
= R1*cos70 + R1*cos20 = G (сумма)
R1*(cos70 + cos20) = G.
Отсюда R1 = G / (cos70 + cos20).
Тут есть 2 варианта решения - подставить значение G. найти табличные значения косинусов и получить результат.
По второму варианту можно искать сумму косинусов двух углов. Но и в таком случае не обойтись без таблицы (калькулятора).
R1 = 350 / ( 0.34202 + 0.939693) = 350 / 1.281713 = 273.0721.