щас
Пошаговое объяснение:
вот пятый класс 739 как и просил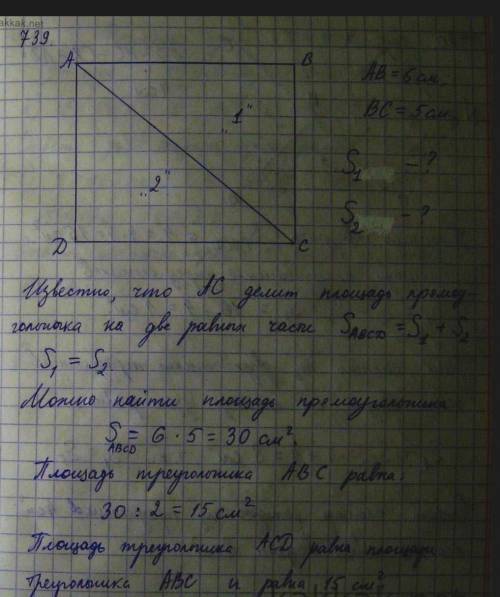
1)2листа разрезали на 3 части.,получилось 2*3=6 листов,так как разрезали 2 листа то 9было-2 разрезанных=7 листов листов целых и (2 разрезанных)+6 листов=15 листов стало.. ответ 2 листа разрезали на 3
2)
малыш-600(г)-6 мин.
карлсон - ? в 2 раза быстрее
всего они вместе(время) - ?
1) 6: 2=3(мин) - карлсон за 3 минуты 600 грамм варенья.
2) 6+3=9(мин) - вместе съедят всё варенье.
3)
пусть федя поймал x пескарей, тогда алеша поймал (x+3), игорь -(x+3)+3=(x+6), валя (x+6)+3=x+9
x+x+3+x+6+x+9=26
4x=8
x=2
федя - 2
алеша 2+3=5
игорь 5+3=8
валя 8+3=11
ответ:
отложим одну монету, а на каждую чашу весов положим по две монеты. возможны два случая.
1) весы в равновесии. так как четырёх настоящих монет нет, то на одной чаше лежат обе фальшивые монеты. следующим взвешиванием достаточно сравнить веса монет с одной чаши: если весы в равновесии, то эти монеты настоящие, и фальшивые монеты в другой чаше; если весы не в равновесии, то фальшивые монеты – на весах.
2) одна из чаш перевесила. тогда на весах находится или только лёгкая фальшивая монета в более лёгкой чаше или только тяжёлая фальшивая монета в более тяжёлой чаше, или обе монеты находятся в разных чашах. вторым взвешиванием сравним веса монет в лёгкой чаше: если весы не в равновесии, то более лёгкая монета – фальшивая. если весы в равновесии, то отложенная монета – фальшивая (и она лёгкая). аналогично, третьим взвешиванием сравним веса монет из тяжёлой чаши: тогда, либо более тяжёлая монета – фальшивая, либо, если весы в равновесии, отложенная монета фальшивая (и она тяжёлая).
решение 2
первый раз положим на чаши весов первую и вторую монеты, а второй раз – третью и четвёртую. возможны только два случая.
1) один раз весы были в равновесии (пусть при первом взвешивании; при этом на чашах настоящие монеты), а другой раз – нет.
возьмем настоящую монету из первого взвешивания и сравним её с той, что оставалась на столе. если их веса равны, то последняя монета настоящая, а фальшивые – те, что участвовали во втором взвешивании. иначе, монета со стола – фальшивая, и мы знаем, легче она настоящей или тяжелее, а потому знаем, лёгкая или тяжёлая фальшивая монета участвовала во втором взвешивании.
2) оба раза весы были не в равновесии. тогда на весах каждый раз была одна фальшивая монета, а на столе осталась настоящая. взвесим её с лёгкой монетой из первого взвешивания. если веса равны, то в первом взвешивании фальшивой была более тяжёлая, а во втором – более лёгкая. если же более лёгкая монета из первого взвешивания оказалась легче, то она фальшивая, а из второго взвешивания фальшивая – более тяжёлая.
замечания
отметим, что решение 2 не использует то, что обе фальшивых монеты весят столько же, сколько две настоящих.
ответ:28
Пошаговое объяснение: