Найдите боковое ребро правильной 4-ех угольной призмы если строна основания 5 а полщадь поверхности 190

👇

Увидеть ответ

Ответ:

Полина1111111С

30.04.2022

если имелась в виду площадь боковой поверхности.

Sбок.поверхности=190 Sбок. грани = 190/4=47,5 длина ребра=9,5

если имелась в виду площадь всей поверхности

Sполн=Sбок+2Sосн

Sосн=5*5=25

Sбок=190-50=140

Sбок.грани=140/4=35

длина ребра=35/5=7

(в основании правильной четырёхугольной призмы лежит квадрат, её боковые грани - равные прямоугольники)

4,4(6 оценок)

Открыть все ответы

Ответ:

statarincev2019

30.04.2022

1.условие
2.решение
3.ответ

1 – 2 класс.Задачи на нахождение суммы.Задачи на увеличение и уменьшение числа на несколько единиц.Задачи на нахождение неизвестного слагаемого.Задачи на нахождение остатка.Задачи на нахождение неизвестного вычитаемого и слагаемого.Задачи на нахождение уменьшаемого.Задачи на разностное сравнение.Задачи с косвенными вопросами.Составные задачи на нахождение суммы.Составные задачи на нахождение остатка.Составные задачи на нахождение слагаемого и вычитаемого.Составные задачи на нахождение «третьего» слагаемого.Составные задачи на нахождение суммы.Составные задачи на нахождение уменьшаемого.Составные задачи на разностное сравнение.
3 класс.Простые задачи на умножение.Задачи на увеличение и уменьшение числа в несколько раз.Задачи на деление по содержанию и на равные части.Задачи на кратное сравнение.Задачи на увеличение и уменьшение числа в несколько раз ( косвенная форма).Составные задачи на нахождение суммы.Задачи на приведение к единице.Составные задачи на нахождение уменьшаемого, вычитаемого, разности.Составные задачи на разностное и кратное сравнение.Задачи на нахождение суммы двух произведений.Задачи на нахождение неизвестного слагаемого.Составные задачи на деление суммы на число и числа на сумму.Составные задачи на цену, количество и стоимость.Задачи на нахождение периметра и сторон геометрических фигур.Задачи на нахождение числа по доле и доли по числу.
4 класс.Простые задачи на движение.Задачи на встречное движение.Задачи на движение в одном направлении.Задачи на противоположное движение и движение в обратном направлении.Задачи на пропорциональное движение.Задачи на нахождение неизвестного по двум разностям.Задачи на нахождение площади.

4,8(74 оценок)

Ответ:

23452345torer

30.04.2022

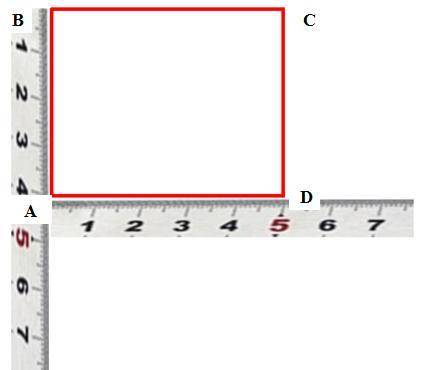
С линейки построим и обозначим вершины через ABCD (см. рисунок 1).

1. Вычислим периметр прямоугольник со сторонами AB=4 см и AD=5 см по формуле периметра:

P=2·(AB + AD)=2·(4 см + 5 см)= 2·9 см= 18 см

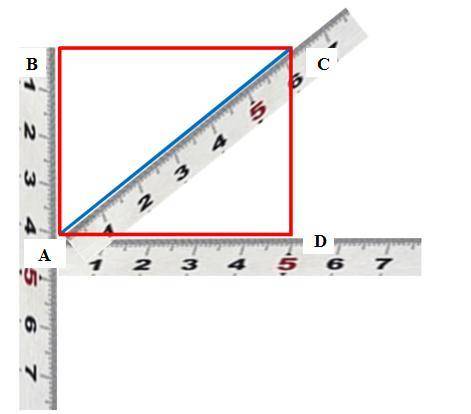
2. Проведем диагональ AC прямоугольника и измерим её (см. рисунок 2). Длина AC равна приблизительно 6,4 см. Тогда, так как 5 < 6,4, то большая сторона прямоугольника AD < AC.

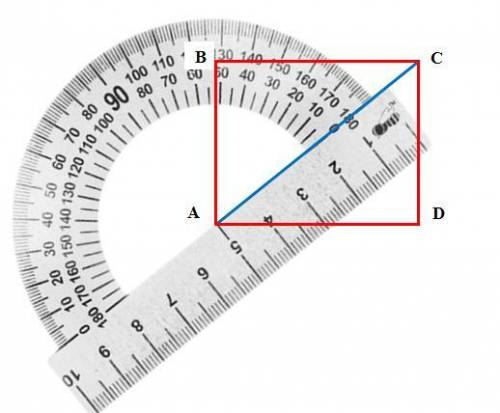
3. С транспортира измерим угол между диагональю и меньшей стороной прямоугольника (см. рисунок 3). Угол составляет приблизительно 52°.