Серик- парикмахер, Даулет- мельник, Ваня- плотник, Илья- маляр, Мади- почтальон.
Пошаговое объяснение:
Из условия можно сделать вывод, что Серик собирается сходить в гости к мельнику, живет вместе с почтальоном и играет вмести с плотником и маляром. Значит Серик- парикмахер
Даулет играет с плотником и маляром и живет вместе с почтальоном. А так как парикмахером является Серик, то Даулет- мельник.
Ваня ходит в гости к почтальону и никогда не держал в руках малярную кисть. Отсюда можно сделать вывод, что он плотник.
Илья ходит в гости к другу почтальону, значит он маляр, а Мади- почтальон.
ответ: 1) сходится 2) сходится 3) сходится
Пошаговое объяснение:
1) Известно, что ряд сумма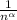
сходится при α > 1
В частности сходится и ряд суммы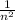
Т.к.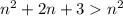
то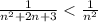
По признаку сравнения для положительных числовых рядов из сходимости ряда с большими членами следует сходимость ряда с меньшими членами.
2) Аргумент синуса убывает от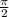
для 0
Следовательно рассматриваемый ряд положителен и для синуса можем записать
sinx < x
Исследуем на сходимость ряд сумм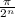
Найдем для него отношение последующего члена к предыдущему
По признаку Даламбера ряд сумм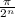
сходится.
По признаку сравнения для положительных числовых рядов из сходимости ряда с большими членами следует сходимость ряда с меньшими членами, т.е сходится и ряд сумм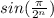
3. Найдем отношение последующего члена к предыдущему
При n стремящемся к бесконечности D стремится к нулю, а следовательно, по признаку Даламбера ряд сходится.