По всей видимости, это практическая работа по экспериментальному нахождению значения числа Пи. Она должна оформляться следующим образом: Берутся несколько окружностей (или тел, имеющих в сечении окружность, например, кастрюля, чашка, тарелка, банка и т п) Далее, измеряется диаметр (линейкой) и длина окружности (ниткой) . После чего длина окружности делится на диаметр. Все эти данные заносятся в таблицу№п/п : Длина окружности : Диаметр : ОтношениеДалее, например, вычисляется среднее арифметическое всех отношений. Оно и будет приближенным значением числа ПИ. Так как точное значение ПИ нам известно, можно найти погрешность (как абсолютную, так и относительную) , ну и прочее.. . Совет : Берите окружности как можно большего диаметра и измеряйте как можно точней (до мм) , тогда полученное отношение будет очень близко к ПИ, то есть 2 знаков после запятой можно добиться, то есть получить примерно 3.14.Вот и всё. Успехов!
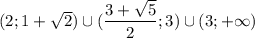
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть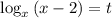 
. Тогда 
:
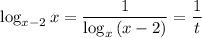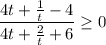. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма 
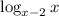равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
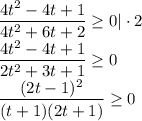
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
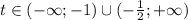
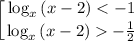
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
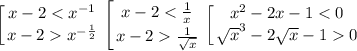
Первое неравенство имеет решение (с учётом ОДЗ)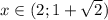 
Второе неравенство раскладывается на множители:
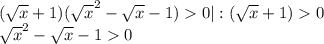
Нули получившегося неравенства: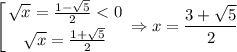 
C учётом ОДЗ получаем, что в данном случае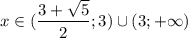 
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
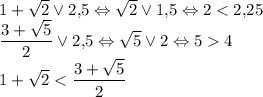
Тогда промежутки не пересекаются, итоговый ответ: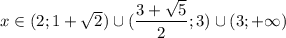 
Пошаговое объяснение:
А - 3
Б - ответа нет, но будет b^21
В - 1