
Высота трапеции = 24.
Пошаговое объяснение:
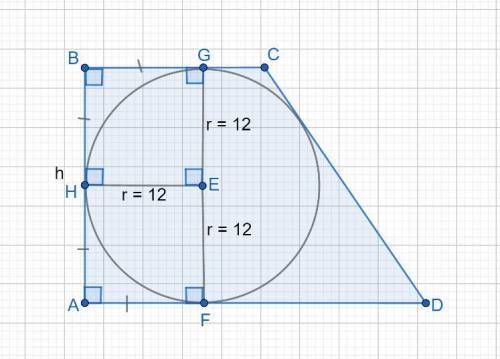
Дано: ABCD - прямоугольная трапеция, r = 12 (радиус вписанной окружности).
Найти высоту трапеции h.
Решение.
т.E - центр вписанной окружности.
Четырехугольник HBGE является квадратом, так как:
∠H = 90°; ∠ G =90° , угол между касательной и радиусом, проведенным в точку касания = 90°,
∠B = 90° по условию трапеция прямоугольная.
Значит ∠E = 90°, сумма углов в четырехугольнике = 360°.
⇒ HBGE прямоугольник.
В прямоугольнике противолежащие стороны равны.
GE = EH, радиусы вписанной окружности.
HB = BG, отрезки касательных проведенных из одной точки до точек касания равны.
⇒ все стороны HBGE равны между собой и равны радиусу вписанной окружности r.
Аналогично, AHEF также является квадратом, со стороной = r.
Тогда высота трапеции h = 2r = 2 * 12 = 24.
Меньшее кол-во = 3
Большее кол-во = 6
Мы знаем, что на каждой мишени должно быть ровно 3 попадания, ни больше, ни меньше, значит общее кол-во попаданий должно делиться на 3.
Федор и Эдуард могли попасть либо 4, либо 5 раз, т.к наибольшее и наименьшее кол-во выстрелов определено.
Значит
3+6+x+y кол-во выстрелов, которое делится на 3.
Предположим, что x=4, y=4
Тогда 3+6+4+4=17 (17 не дел. на 3, значит ответ неверный и Федор с Эдуардом точно не сделали по 4 точных выстрела)
Предположим, что x=5,y=5
Тогда 3+6+5+5=19 (аналогично, Эдуард и Федор не сделали по 5 точных выстрелов)
Остается вариант, когда x=4, y=5 (или наоборот, в данном случае это не имеет значения)
3+6+4+5=18
18:3=6
ответ: 6 мишеней было поражено
1.1,2,3,4,5,6,7,8,9
2.11,22,33,44,55,66,77,88,99