ЗАДАНИЯ 1. Прямая a пересекает плоскость β в точке C, и образует с плоскостью угол 60°. P∈a, точка R - проекция точки P на плоскость β. PC=14 см. Найди RC.
2. К плоскости α проведена наклонная, длина которой равна 26 см, проекция наклонной равна 10 см . На каком расстоянии от плоскости находится точка, из которой проведена наклонная?
3. К плоскости α проведена наклонная AB (A∈α). Длина наклонной равна 8 см, наклонная с плоскостью образует угол 45°. Вычисли, на каком расстоянии от плоскости находится точка B.
4. Наклонная AD с плоскостью α образует угол 300, а наклонная DC с плоскостью α образует угол 450. Длина перпендикуляра DB равна 28 см. Вычисли длины обеих наклонных.
5. Длина отрезка VB равна 20 м. Он пересекает плоскость в точке O. Расстояние от концов отрезка до плоскости соответственно равны 8 м и 2 м. Найди острый угол, который образует отрезок VB с плоскостью.
6. Проекции наклонных AD и DC на плоскости α равны соответственно 8 см и 8 см, а угол между ними равен 120°.
Вычисли расстояние между концами проекций наклонных.
7. Равнобедренный треугольник ABE находится в плоскости α. Боковые стороны треугольника ABE равны по 20 см, а сторона основания AE=32 см. К этой плоскости проведены перпендикуляр CB, который равен 9 см, и наклонные CA и CE. Вычислите расстояние от точки C до стороны треугольника AE.
8. Прямоугольный треугольник MBE (∢M=90°) находится в плоскости α. BE=13 см, а ME=5 см. К этой плоскости проведён перпендикуляр CB длиной 5 см. Вычисли расстояние от точки C до стороны треугольника ME.
РЕШИТЬ ОСТАЛОСЬ 2 ДНЯ
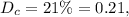 а долю масла в сливках, как
а долю масла в сливках, как 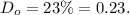
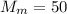 кг молока. Посчитаем, какую массу масла
кг молока. Посчитаем, какую массу масла 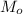 можно из него получить.
можно из него получить.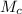 , которую можно собрать с молока, воспользуемся простым правилом: умножаем на число процентов в доле и делим на сто процентов:
, которую можно собрать с молока, воспользуемся простым правилом: умножаем на число процентов в доле и делим на сто процентов: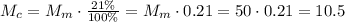 кг.
кг.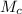 мы просто умножили
мы просто умножили 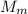 на
на 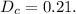
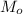 , которую можно выделить из собранных сливок, воспользуемся теми же правилами:
, которую можно выделить из собранных сливок, воспользуемся теми же правилами: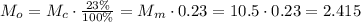 кг масла
кг масла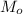 мы просто умножили
мы просто умножили 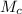 на
на 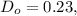 т.е., учитывая расчёт **(A)** мы умножили
т.е., учитывая расчёт **(A)** мы умножили 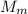 на
на 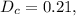 а затем на
а затем на 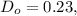 и в самом деле:
и в самом деле: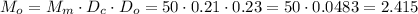 кг масла
кг масла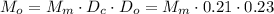 ;
;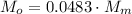 ;
;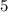 кг
кг 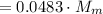 ;
;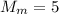 кг
кг 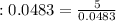 кг
кг 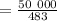 кг ;
кг ;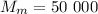 кг
кг 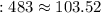 кг ;
кг ;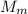 из уравнения **(С)** :
из уравнения **(С)** :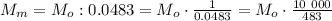 и опять же найдем, что:
и опять же найдем, что: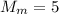 кг
кг 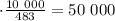 кг
кг 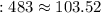 кг ;
кг ;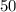 кг молока можно получить
кг молока можно получить 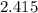 кг масла.
кг масла.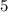 кг масла нужно
кг масла нужно 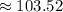 кг молока.
кг молока.
Прежде чем вычислить сумму квадратов этих чисел,
найдём эти числа, для этого обозначим эти числа за (х) и (у),
тогда согласно условия задачи:
х+у=15 (1)
Средне-арифметическое этих двух чисел равно:
(х+у)/2
Средне геометрическое этих двух чисел равно:
√(х*у)
25% средне геометрического числа равно:
25% *√(ху) :100%=0,25*√(ху)=0,25√(ху)
Согласно условия задачи составим второе уравнение:
(х+у)/2 - √(ху)=0,25√(ху)
(х+у)/2=0,25√(ху)+√(ху)
(х+у)/2=1,25√(ху)
(х+у)=2*1,25√(ху)
х+у=2,5√(ху) (2)
Решим получившуюся систему из двух уравнений:
х+у=15
х+у=2,5√(ху)
Из первого уравнения системы уравнений найдём значение (х)
х=15-у -подставим значение (х) во второе уравнение
15-у+у=2,5√[(15-y)*y]
15=2,5√(15y-y²) чтобы избавиться от иррациональности в правой части, возведём левую и правую части уравнения в квадрат:
225=6,25*(15у-у²)
225=93,75у-6,25у²
6,25у²-93,75у+225=0
у1,2=(93,75+-D)/2*6,25
D=√(93,75² -4*6,25*225)=√(8789,0625-5625)=√3164,0625=56.25
у1,2=(93,75+-56,25)/12,5
у1=(93,75+56,26)/12,5=150/12,5=12
у2=(93,75-56,25)/12,5=37,5/12,5=3
Подставим значения (у1) и (у2) в х=15-у
х1=15-12=3
х2=15-3=12
Из получившихся чисел можно сделать вывод, что эти два числа 12 и 3
Отсюда сумма квадратов этих чисел равна:
12²+3²=144+9=153
ответ: 153