
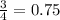
Пошаговое объяснение:
В принципе, решение можно осуществить 2 путями. Для начала, обозначим вероятности
Pн - нечетное произведение очков,
Рч - четное произведение очков
1. При двух бросках в результате могут быть только 2 вероятных события:
- четное произведение очков
- нечетное произведение очков.
Эти 2 случая охватывают полностью возможные наступления событий.
Соответственно, верно равенство
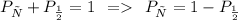
Произведение 2 чисел будет НЕчетным тогда, когда НЕчетными являются ОДНОВРЕМЕННО ОБА из множителей.
Два броска являются независимыми (результат 2 броска не зависит от числа, выпавшего первым);
Из равновероятных 6 событий для одного броска нечетныеэми будут 3.
Следовательно, вероятность нечетного броска равна 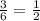
Вероятность того, что произведение чисел бросков будет нечетным равна вероятности двойного нечетного броска - т.е. произведению вероятностей для 1 и 2 броска:
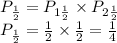
Следовательно, вероятность того, что произведение чисел бросков будет четным равна разности между 1 и Рн:
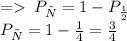
2. Возможны варианты бросков (первый-второй броски):
1 - чч - четный-четный
2 - чн - четный-нечетный
3 - нч - нечетный-четный
4 - нн - нечетный-нечетный.
Произведение же четно, когда четным является ХОТЯ БЫ ОДИН из множителей.
А это происходит в трех случаях из 4-х - случае 1, 2 и 3 из указанных выше.
То есть
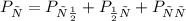
Легко проверить, что вероятность наступления каждого из событий равна:
произведению вероятности четности/нечетности первого броска на вероятность четности/нечетности второго броска.
Для любого броска вероятность четного числа очков равна вероятности нечетного и составляет 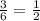
Следовательно:
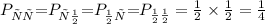
А значит,
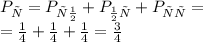
Итак, в двух различных решениях получили одинаковые результаты. Следовательно, ответ верен:
ответ : 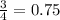
Математическое ожидание случайной величины Х, имеющей гипергеометрическое распределение, и ее дисперсия равны:
ПРИМЕР №1. В урне 2 белых и 3 черных шара. Шары наудачу достают из урны без возвращения до тех пор, пока не появится белый шар. Как только это произойдет, процесс прекращается. Составить таблицу распределения случайной величины X – числа произведенных опытов, найти F(x), P(X ≤ 2), M(X), D(X).·
Решение: Обозначим через А – появление белого шара. Опыт может быть проведен только один раз, если белый шар появится сразу:. Если же в первый раз белый шар не появился, а появился при втором извлечении, то X=2. Вероятность такого события равна . Аналогично: , , . Запишем данные в таблицу:
X 1 2 3 4
P 0,4 0,3 0,2 0,1
НайдемF(x):
Найдем P(X ≤ 2) = P(X = 1 или X = 2) = 0,4 + 0,3 = 0,7
M(X) = 1 · 0,4 + 2 · 0,3 +3 · 0,2 + 4 · 0,1 = 2.
D(X) = (1-2)2 · 0,4 + (2-2)2 · 0,3 +(3-2)2 · 0,2 + (4-2)2 · 0,1 = 1
Пошаговое объяснение: