Арифметическая прогрессия состоит из четырёх различных чисел. Известно, что если заменить в ней третье число на единицу, то получится геометрические прогрессия. Найти исходную прогрессию.

👇

Увидеть ответ

Ответ:

BcezHaNKa

29.12.2022

Пошаговое объяснение:

Для начала парочка примеров. Рассмотрим несколько наборов чисел:

1; 2; 3; 4; ...

15; 20; 25; 30; ...

Что общего у всех этих наборов? На первый взгляд — ничего. Но на самом деле кое-что есть. А именно: каждый следующий элемент отличается от предыдущего на одно и то же число.

4,8(47 оценок)

Открыть все ответы

Ответ:

tayasivakova

29.12.2022

Відповідь:

$X=\left[\begin{array}{ccc}-\frac{3}{2} &4&1\\3&-6&-1\\-\frac{5}{4} &\frac{9}{2} &\frac{3}{2} \end{array}\right]$

Покрокове пояснення:

$A=\left[\begin{array}{ccc}-1&1&2\\2&1&0\\-3&-1&2\end{array}\right] \\$ $B=\left[\begin{array}{ccc}2&-1&1\\0&2&1\\-1&3&1\end{array}\right] \\$

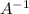
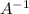Щоб розв'язати матричне рівняння АХ=В треба помножити ліву і праву частину на обернену матрицю $A^{-1}$

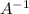$A^{-1}$ АХ= $A^{-1}$ В (Оскільки 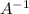$A^{-1}$ А=Е)

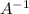ЕХ= $A^{-1}$ В (Е - одинична матриця)

Х=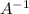 $A^{-1}$ В

Отож, для початку перевіримо, чи матриця невироджена, для цього знайдемо визначник

det A = (-1)·1·2 + 1·0·(-3) + 2·2·(-1) - 2·1·(-3) - (-1)·0·(-1) - 1·2·2 =-2+0-4+6-0-4=-4

Матриця невироджена, значить існує обернена матриця 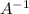$A^{-1}$ , знайдемо її:

Транспонуємо її:

$A^T=\left[\begin{array}{ccc}-1&2&-3\\1&1&-1\\2&0&2\end{array}\right]$

Тепер знайдемо алгебраїчні доповнення:

$A_{1,1}=(-1)^{1+1}\left[\begin{array}{ccc}1&-1\\0&2\end{array}\right] =(1*2 - 0*(-1)) = 2\\A_{1,2}=(-1)^{1+2}\left[\begin{array}{ccc}1&-1\\2&2\end{array}\right] = -(1*2 - 2*(-1)) = -4\\A_{1,3}=(-1)^{1+3}\left[\begin{array}{ccc}1&-1\\2&0\end{array}\right] = (1*0 - 2*1) = -2\\A_{2,1}=(-1)^{2+1}\left[\begin{array}{ccc}2&-3\\0&2\end{array}\right] = -(2*2 - 0*(-3)) = -4\\A_{2,2}=(-1)^{2+2}\left[\begin{array}{ccc}-1&-3\\2&2\end{array}\right] = ((-1)*2 - 2*(-3)) = 4\\$

$A_{2,3}=(-1)^{2+3}\left[\begin{array}{ccc}-1&2\\2&0\end{array}\right] = -((-1)*0 - 2*2) = 4\\A_{3,1}=(-1)^{3+1}\left[\begin{array}{ccc}2&-3\\1&-1\end{array}\right] = (2*(-1) - 1*(-3)) = 1\\A_{3,2}=(-1)^{3+2}\left[\begin{array}{ccc}-1&-3\\1&-1\end{array}\right] = -((-1)*(-1) - 1*(-3)) = -4\\A_{3,3}=(-1)^{3+3}\left[\begin{array}{ccc}-1&2\\1&1\end{array}\right] = ((-1)*1 - 1*2) = -3$

Тоді обернена матриця буде мати такий вигляд:

$A^{-1}=-\frac{1}{4} \left[\begin{array}{ccc}2&-4&-2\\-4&4&4\\1&-4&-3\end{array}\right]$

Тоді матрицю Х=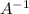 $A^{-1}$ В шукаємо так:

$X=-\frac{1}{4} \left[\begin{array}{ccc}2&-4&-2\\-4&4&4\\1&-4&-3\end{array}\right] *\left[\begin{array}{ccc}2&-1&1\\0&2&1\\-1&3&1\end{array}\right]=-\frac{1}{4} \left[\begin{array}{ccc}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\end{array}\right]$

(Знаходження кожного елемента я напишу окремо, щоб не було дуже громіздко)

х₁₁ = 2 · 2 + (-4) · 0 + (-2) · (-1) = 4 + 0 + 2 = 6

х₁₂ = 2 · (-1) + (-4) · 2 + (-2) · 3 = (-2) - 8 - 6 = -16

х₁₃ = 2 · 1 + (-4) · 1 + (-2) · 1 = 2 - 4 - 2 = -4

х₂₁ = (-4) · 2 + 4 · 0 + 4 · (-1) = (-8) + 0 - 4 = -12

х₂₂ = (-4) · (-1) + 4 · 2 + 4 · 3 = 4 + 8 + 12 = 24

х₂₃ = (-4) · 1 + 4 · 1 + 4 · 1 = (-4) + 4 + 4 = 4

х₃₁ = 1 · 2 + (-4) · 0 + (-3) · (-1) = 2 + 0 + 3 = 5

х₃₂ = 1 · (-1) + (-4) · 2 + (-3) · 3 = (-1) - 8 - 9 = -18

х₃₃ = 1 · 1 + (-4) · 1 + (-3) · 1 = 1 - 4 - 3 = -6

Тоді Х дорівнює

$X=-\frac{1}{4} \left[\begin{array}{ccc}6&-16&-4\\-12&24&4\\5&-18&-6\end{array}\right] =\left[\begin{array}{ccc}-\frac{3}{2} &4&1\\3&-6&-1\\-\frac{5}{4} &\frac{9}{2} &\frac{3}{2} \end{array}\right]$

#SPJ1

4,8(55 оценок)

Ответ:

королева5720

29.12.2022

3) у=3х-1

Пошаговое объяснение:

Для того, чтобы проверить какая из формул задаёт график функции, необходимо взять две точки на графике, подставить в формулы координаты х и у этих точек, и проверить, выполняется ли равенство.

Возьмём точки с координатами (0;1) и (1;4) принадлежащие графику.

1) у=-3х+1

(0;1):

1=-3*0+1

1=1 - верно.

(1;4):

4=-3*1+1

4=-2 - неверно

⇒ у=-3х+1 - не задаёт график функции.

2) у=х

Известно, что функция у=х задаёт прямую, проходящую через начало координат, нам не подходит.

3) у=3х-1