

1) 23
2) 5,5
3) 1,5
Пошаговое объяснение:
1) (3 1/5 - 1 2/3) * 15
сначала раскроем скобку
(3 1/5 - 1 2/3) * 15 = (16/5 - 5/3) * 15 = (48/15 - 25/15) * 15 = 23/15 * 15
23/15 * 15 = 23/15 * 15/1 = 23
2) (2 3/7 + 1 1/2) : 5/7
сначала раскроем скобку
(2 3/7 + 1 1/2) : 5/7 = (17/7 + 3/2) : 5/7 = (34/14 + 21/14) : 5/7 = 55/14 : 5/7
55/14 : 5/7 = 55/14 * 7/5 = 11/2 = 5 1/2 = 5,5
3) (5 2/5 + 9 1/6) : 9 32/45
сначала раскроем скобку
(5 2/5 + 9 1/6) : 9 32/45 = (27/5 + 55/6) : 9 32/45 = (162/30 + 275/30) : 9 32/45 = 437/30 : 9 32/45
437/30 : 9 32/45 = 437/30 : 437/45 = 437/30 * 45/437 = 45/30 = 3/2 = 1 1/2 = 1,5
В решении.
Пошаговое объяснение:
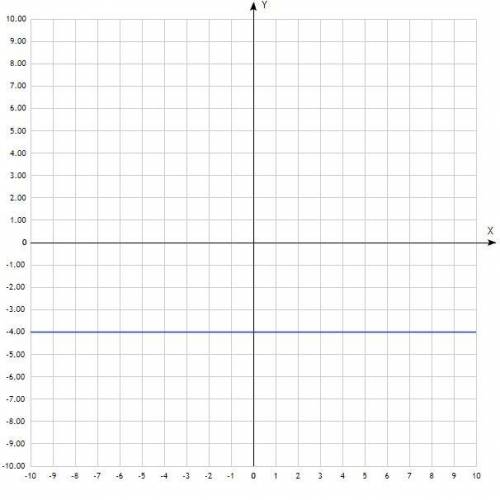
1) f(x) = -4;
График - прямая линия, параллельная оси Ох, проходит через точку у = -4;
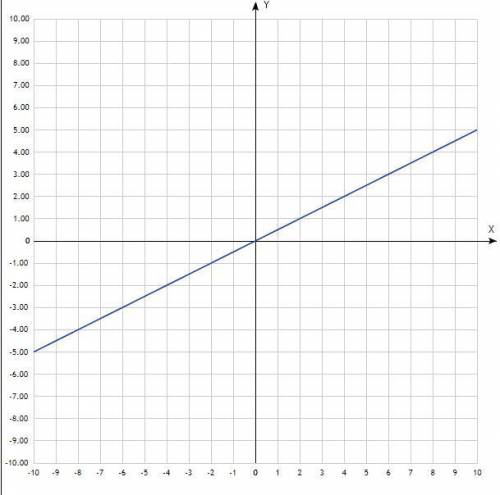
2) f(x) = 1/2 х, или 0,5х;
График - прямая линия, проходит через начало координат. Придать значения х, вычислить значения у, записать в таблицу:
Таблица:
х -2 0 2
у -1 0 1
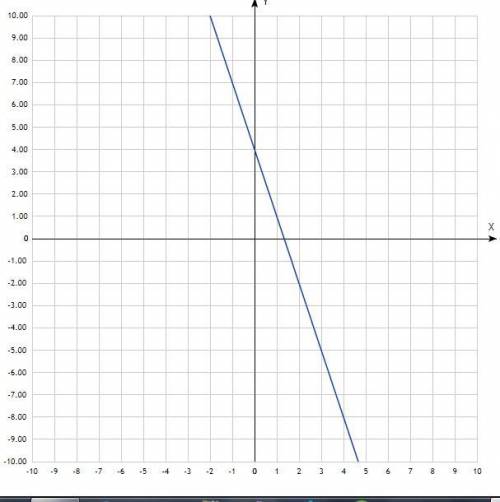
3) f(x) = -3х + 4.
График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -1 0 1
у 7 4 1
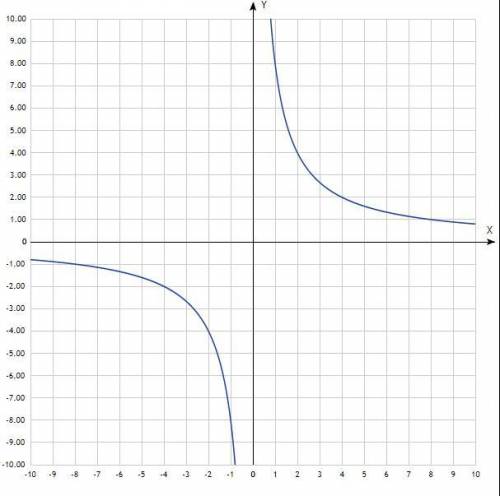
4) f(x) = 8/х
График - гипербола. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -8 -4 -2 -1 1 2 4 8
у -1 -2 -4 -8 8 4 2 1
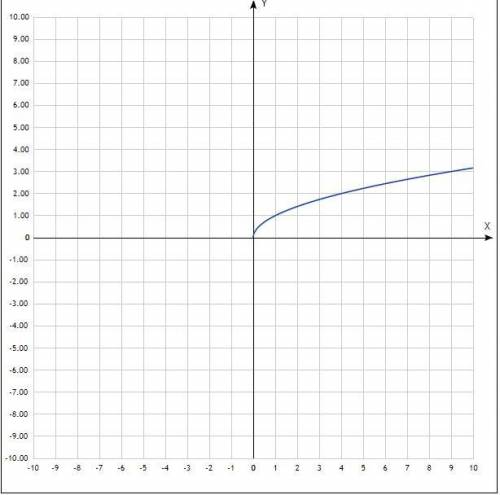
5) f(x) = √х.
Функция √x - один из частных случаев степенной функции. Эта функция не имеет своего собственного имени.
График функции y = √х - ветвь параболы.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х 0 1 4 9
у 0 1 2 3
Пошаговое объяснение:
всего деталей n=300+200+100=600
p1=300/600=1/2-вероятность того, что деталь первого сорта
р2=200/600=1/3-вероятность того, что деталь второго сорта
р3=100/600=1/6-вероятность того, что деталь третьего сорта
из условия находим:
q1=2/100=1/50- вероятность того, что деталь первого сорта будет бракованной
q2=4/100=1/25-вероятность того, что деталь второго сорта будет бракованной
q3=5/100=1/20-вероятность того, что деталь третьего сорта будет бракованной
а) по формуле полной вероятности:
р=p1q1+p2q2+p3q3=1/2×1/50+1/3×1/25+1/6×1/20=19/600≈0.032-
вероятность того, что взятая наугад деталь будет бракованной
б) по формуле Байеса:
р1 =p1q1/p=1/100×600/19=6/19≈0.316- вероятность того, что взятая наугад бракованная деталь принадлежит первой группе