
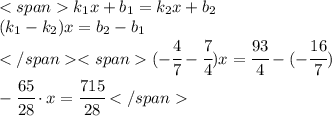
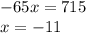
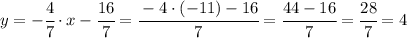
60 кустов.
Пошаговое объяснение:
Примем число всех кустов за 1, тогда
1. 1 - 3/5 = 2/5 (кустов) - остаток.
2. 3/8•2/5 = 3/20 (всех кустов) посадил Павел.
3. 2/5 - 3/20 = 8/20 - 3/20 = 5/20 = 1/4 (всех кустов) посадил Дмитрий.
4. 15 кустов - это 1/4 всех имевшихся кустов, тогда
15 : 1/4 = 15 • 4/1 = 60 (кустов) было всего.
Проверим полученный результат:
Всего - 60 кустов
Пётр посадил 60•3/5 = 36 (кустов)
60 - 36 = 24 (куста) осталось после Петра.
24•3/8 = 9 (кустов) посадил Павел
24 - 9 = 15 (кустов) посадил Дмитрий, верно.
3.
угол принадлежит 2 четверти, синус положительный, косинус и тангенс отрицательные.
Используем формулу:
4.
угол принадлежит 3 четверти, косинус отрицательный.