Пусть прямая а лежит в плоскости α , прямая в лежит в плоскости β. Прямые а и в параллельны. Плоскости α и β пересекаются по прямой с. Прямая а и с лежат в пл.α.Они параллельны, так как прямая а || пл.β (сущуствует прямая b в плоскости β, параллельная a), то прямая а не пересекается с прямой с , лежащей в плоскости β (как линия пересечения пл.α и пл. β), а значит a||c. Аналогично, прямая b || пл.α, так как существует в этой плоскости прямая a, параллельная b.Значит, прямая b не имеет общих точек с пл.α и с прямой с, лежащей в плоскости α ( прямая с - линия пересечения двух плоскостей-одновременно принадлежит и пл.α и пл. β).Поэтому b||c.
Дискриминант выражается формулой: D = b^2 - 4ac. Если a, b, c - целые, то D может заканчиваться только определёнными двумя цифрами. По сути задача стоит так: Если из квадрата целого числа вычесть число, кратное 4, то какие числа от 20 до 40 могут получиться? Решение. Квадраты могут заканчиваться двумя такими цифрами: 00; 01; 04; 09; 16; 21; 24; 25; 29; 36; 41; 44; 49; 56; 61; 64; 69; 76; 81; 84; 89; 96. Чтобы в этом убедиться, достаточно посмотреть таблицу квадратов двузначных чисел. Число, кратное 4, кончается на две цифры, кратные 4: 00; 04; 08; 12; 16; 20; ...; 96. Я не буду их все выписывать, смысла нет. Разность квадрата и числа, кратного 4, могут быть такими: 20=36-16; 21=121-100; 24=324-300; 25=225-200; 28=256-228; 29=169-140; 32=36-4; 33=169-136; 36=256-220; 37=169-132; 40=144-104. Чему равны a, b, c в каждом случае - сами подумайте. Например, при 20=36-16=6^2-4*1*4 будет a=1; b=6; c=4. Как видим, нельзя выразить числа вида 4n+2 и 4n+3, а можно вида 4n и 4n+1.
При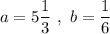 :
: