Посчитаем сколько всего человек в классе.
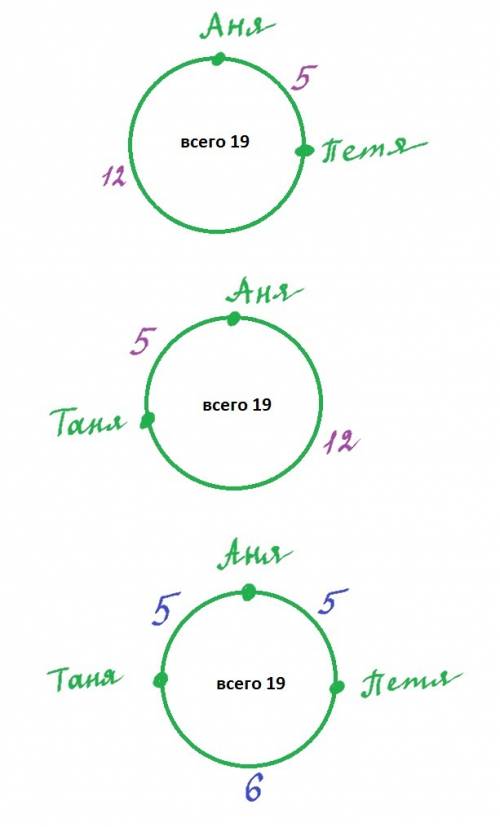
Между Аней и Петей с одной стороны 5 детей, с другой 12 детей, да еще нужно посчитать самих Аню и Петю, т.е. двух человек (смотри рисунок к задаче).
Итого, 12+5+2 = 19 детей в классе.
Посчитаем сколько детей между Петей и Таней.
От Тани до Ани всего 12 детей. Это все, кто стоит от Ани до Пети, от Пети до Тани да еще сам Петя.
От Ани до Пети 5 детей, да еще один Петя - это 6 детей.
12-6 = 6 детей стоит между Петей и Таней.
ответ: всего в классе 19 детей, между Петей и Таней 6 детей.
1. (2) - тире перед обобщающим словом.
Весь лес стал полниться чуть слышными шорохами, хрупким хрустом - звуками (об.сл.) неодушевлённой жизни. И каждый звук был сам по себе: то хруст ветвей, то звон капель, то посвисты жёстких хвоинок.
2. (2) и (3) - запятые при обособленном обстоятельсве, (4) и (5) - запятые при однородных определениях.
Пробуждается зарянка рано утром и поёт тихонько, как будто спросонья, свою тонкую,звонкую, замирающую в конце песенку.
3. (2) - запятая при обособленном определении, (4) - запятая при однородных определениях, (5) - запятая при дееприч. обороте.
Возникла и полилась тихо песня, полная робкой радости и светлой, весенней грусти. Это запела зарянка, пробудившись ранним утром.
4. (1) и (2) - запятые при однородных подлежащих, (6) и (7) запятая при обособленном обстоятельстве.
Но вдруг отдельные звоны, свисты, хрусты чудесно соединились и зазвучали слаженно и живо. И вот возникла, как живая струйка воды, лесная песенка.
Линейное уравнение — это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна 1. Линейное уравнение можно представить:
в общей форме, в канонической форме.
Линейное уравнение от одной переменной можно привести к виду: Линейное уравнение одной переменной.
Количество решений зависит от параметров a и b.
Если а=в=0 , то уравнение имеет бесконечное множество решений, поскольку х*0=0
Если а=0 в не=0 , то уравнение не имеет решений, поскольку х=-в не=0
Если а не=0 , то уравнение имеет единственное решение х=-в/а
Линейное уравнение двух переменных. Геометрическое место точек линейного уравнения от двух переменных вида:
y = ax + b.
Линейное уравнение двух переменных можно представить
в общей форме: в канонической форме: в форме линейной функции: , где
Решением или корнями такого уравнения называют такую пару значений переменных , которая обращает его в тождество. Таких решений (корней) линейное уравнение с двумя переменными имеет бесконечное множество. Геометрической моделью (графиком) такого уравнения является прямая .