Пошаговое объяснение:
4) -1,4 + 0,5(11b – 2)< -5,5b + 1,6
-1,4+5,5b-1<1,6-5,5b
5,5b-2,4<1,6-5,5b
5,5b+5,5b<2,4+1,6
11b<4; b<4/11; b∈(-∞; 4/11)
5) 5 2/3+7/3 (14х – 3) > 4/9(18x — 2)
5 2/3 +32 2/3 ·x-7>8x -8/9
32 2/3 ·x-1 1/3>8x -8/9
32 2/3 ·x-8x>1 3/9 -8/9
24 2/3 ·x>4/9
x>4/9 ·3/74; x> 2/(3·37); x>2/111; x∈(2/111; +∞)
6) 5/6 (7 + 9y) < 14 2/3-7/8 (5y — 8)
5 5/6 +7 1/2 ·y<14 2/3 -4 3/8 ·y+7
5 5/6 +7 1/2 ·y<21 2/3 -4 3/8 ·y
7 4/8 ·y+4 3/8 ·y<21 4/6 -5 5/6
11 7/8 ·y<15 5/6
y< 95/6 ·8/95; y<4/3; y<1 1/3; y∈(-∞; 1 1/3)
Если одна прямая расположена в плоскости а, а другая прямая пересекает эту плоскость, то Через эти прямые прямые нельзя провести две различные плоскости.
p.s. остальные возможности перепробовала. Вот вам ещё пример из учебника.
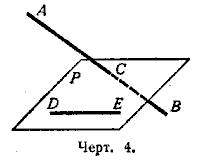
Две прямые могут быть расположены в пространстве так, что через них нельзя провести плоскость.
Возьмём, например, две такие прямые АВ и DЕ, из которых одна пересекает некоторую плоскость Р, а другая лежит на ней, но не проходит через точку (С) пересечения первой прямой и плоскости Р.Через такие две прямые нельзя провести плоскость, потому что в противном случае через прямую и точку С проходили бы две различные плоскости: одна Р, пересекающая прямую АВ, и другая, содержащая её, а это невозможно.
10 ⁸/₁₅
Решение на фото
Пошаговое объяснение: