Возрастает на (-∞;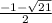
), дальше убывает на (
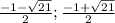) и снова возрастает на (
;+∞).
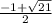Пошаговое объяснение:
Найдём производную исходной функции, пользуясь правилами дифференцирования:
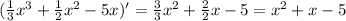
Чтобы найти промежутки монотонности, найдём точки смены монотонности. Они достигаются при равенстве производной нулю. Решим соответствующее уравнение:
⇔ 
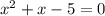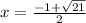или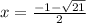 
.
Так мы получили точки смены монотонности. Очевидно, что функция возрастает на промежутке (-∞;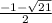) - это легко показать на конкретных значениях, а значит можно восстановить все остальные промежутки так, как показано в ответе.
3. При каких условий неравенство ax*2 +bx+c> 0 не выполняется ни при каком действительном значении х?
А) <0; D<0 B) a>0; D_<0 C) a>0; D>0
D) а<0; D>0 E) a<0; D_<0
Пошаговое объяснение:
у=ax² +bx+c . Графиком является парабола ,для которой у должен быть всегда отрицательным . Это возможно если парабола находится ниже оси ох и ее ветви направлены вниз (чтобы не пересекать ось ох).
Чтобы ветви были вниз : а<0,
Чтобы не пересекала ось ох , не долно быть корней квадратного трехчлена : D<0/