Длина прямоугольника равна 13 см.
Пошаговое объяснение:
Пусть х - ширина прямоугольника, тогда (х+3) - длина прямоугольника.
Площадь прямоугольника равна (х+3)*х см²
После увеличения длины на 2 см и ширины на 1 см, измерения прямоугольника стали равны: длина х+3+2=х+5 (см) , ширина х+1 (см).
Площадь полученного прямоугольника равна (х+5)(х+1) см².
По условию, площадь полученного прямоугольника больше площади исходного прямоугольника на 35 см². Составим уравнение:
(х+5)(х+1)=(х+3)*х=35
x²+6x+5=x²+3x+35
6x-3x=30-5
3х=30
х=30:3
x=10 (см) - ширина прямоугольника
х+3=10+3=13 (см) - длина прямоугольника
наименьшее = 0; наибольшее = 1.5
Пошаговое объяснение:
Найдем производную функции. Это можно сделать по определению через предел от приращения функции деленного на приращение аргумента при дельта x стремящемся к 0 или же по выведенным формулам.
Я сделаю сначала по определению:

Теперь по формулам:
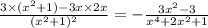
Как видишь вышло то же самое.
Теперь приравняем полученное к 0 и найдем критические точки:
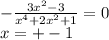
Для себя подставим точку меньше -1; от -1 до 1; больше 1 и получим, что функция возрастает на [-1; 1], а на остальных соответственно убывает.
Просчитаем значения функции в точках 0; 1; 5. При x=0, y=0; При x=1, y=1.5; При x=5, y=15/26. Тогда наименьшее значение функции на отрезке [0; 5] равно 0, а наибольшее 1.5
Запишем пропорции в виде равенства дробей.
1) Да, это пропорции, т.к. 51*20=60*17, а (51+17)*20=(60+20)*17.
2) Связь следующая: во второй пропорции к числителям прибавляются знаменатели, в первой же такого нет.
3) На основе первой пропорции можно сделать следующее предположение:
Если в знаменателях поменять местами последние числа, от первого знаменателя отнять первое число второго числителя, из второго числителя вычесть первый, полученный результат вычесть из первого числителя, а после этого поменять местами второй числитель и второй знаменатель, то получится равная пропорция: 42/4=27/9