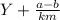, где Y - количество целых, а - все цифры после запятой, включая цифры периода (если после запятой идет ноль он отбрасывается. Например 0,5(3) а=53 и 0,05(3) а=53. b - все цифры стоящие после запятой, но до периода (ноль после запятой, аналогично а отбрасывается). к - количество цифр 9 равное количеству цифр в периоде, m - количество 0 равное количеству цифр, стоящих после запятой, но до периода.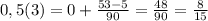
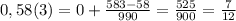
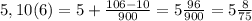
35 градусов
Пошаговое объяснение:
Достроим данную фигуру до треугольника, проведя прямую AC, а точкой D обозначим вершину угла в 60 градусов. Обозначим градусную меру угла CAD буквой a, а угол ACD - буквой b. Тогда сумму углов треугольника ABC можно найти как сумму углов ABC = x, BAC = BAD + CAD = 15 + a и BCA = BCD + ACD = 10 + b. Поскольку сумма углов треугольника равна 180 градусов, то можно составить уравнение:
x + 15 + a + 10 + b = 180
Упростим его:
x + 25 + ( a + b ) = 180
Аналогично в треугольнике ACD, сумма углов треугольника ACD равна сумме углов CAD = a, ACD = b и ADC = 60. Тогда
( a + b ) + 60 = 180
Поскольку в обоих уравнениях правые части одинаковы, то можно приравнять их левые части:
x + 25 + ( a + b ) = ( a + b ) + 60
x + 25 = 60
x = 60 - 25
x = 35