Традиционная шахматная доска представляет собой поле 8 × 8 (всего 64) чередующихся тёмных и светлых клеток (полей).
Рассмотрим первый столбик :
первый вырезать в первом столбце первые три клетки (1,2,3);
второй вырезать в первом столбце 2, 3, 4 клетки;
третий вырезать в первом столбце 3, 4, 5 клетки;
четвертый вырезать в первом столбце 4, 5, 6 клетки;
пятый вырезать в первом столбце 5, 6, 7 клетки;
шестой вырезать в первом столбце 6, 7, 8 клетки;
Вывод: в первом столбце прямоугольник 1х3, можно вырезать шестью в шахматной доске 8 столбцов, значит существует, что бы вырезать прямоугольник 1х3 в столбцах.
рассмотрим первую строчку
первый вырезать в первой строке первые три клетки (1,2,3);
второй вырезать в первой строке 2, 3, 4 клетки;
третий вырезать в первой строке 3, 4, 5 клетки;
четвертый вырезать в первой строке 4, 5, 6 клетки;
пятый вырезать в первой строке 5, 6, 7 клетки;
шестой вырезать в первой строке 6, 7, 8 клетки.
Вывод: в первой строке прямоугольник 1х3, можно вырезать шестью в шахматной доске 8 строк, значит существует, что бы вырезать прямоугольник 1х3 в строчках.
сколькими можно вырезать из шахматной доски прямоугольник 1х3?
для этого сложим количество в столбцах и количество в строках существует вырезать прямоугольник 1х3 из шахматной доски.
ответ: Существует
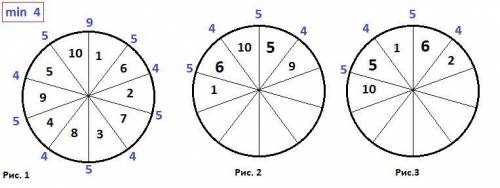
4 - наибольшее возможное значение величины, равной наименьшей из разностей между номерами соседних (по кругу) секторов. Один из вариантов расположения номеров секторов на рис.1.
5 и более получить невозможно, так как для числа 5 с одной стороны можно расположить сектор с номером 10 (10-5=5), а с другой стороны получить разность, более 4, нельзя, так как 5-1=4 и 9-5=4.
Аналогично для числа 6. Если с одной стороны можно получить разность 6-1=5, то с другой стороны более 4 не получится, так как 10-6=4 и 6-2=4. Рис.2 и рис.3