94,5 км/час - скорость мотоциклиста
Пошаговое объяснение:
1 вариант решения:
По условию задания дано:
V = 24,5 км/ч - скорость велосипедиста
t = 3/5 ч - мотоциклист догонит велосипедиста
Найти: V мотоциклиста
1. 24,5 * 3/5 = 245/10 * 3/5 = 14,7 (км) проедет велосипедист за 3/5 часа
2. 42 + 14,7 = 56,7 (км) необходимо проехать мотоциклисту
3. 56,7 : 3/5 = 567/10 * 5/3 = 567/6 = 94,5 (км/час) - скорость мотоциклиста
2 вариант решения:
1. 42 км : 3/5 ч = 70 км/час - скорость сближения мотоциклиста с велосипедистом
2. 70 км/час + 24,5 км/час = 94,5 км/час - скорость мотоциклиста
(см. объяснение)
Пошаговое объяснение:
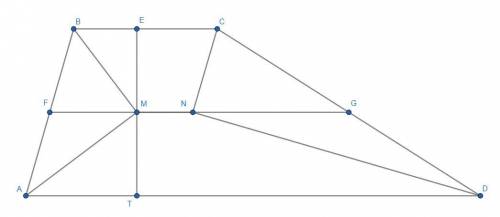
Покажем сначала, что биссектрисы AM и BM пересекаются под прямым углом. Действительно, пусть ∠ABC=α и ∠BAD=β. Тогда α+β=180°. Так как биссектриса делит угол пополам, то верно, что ∠ABM+∠BAM=α/2+β/2=90°, поэтому и ∠BMA=90°.
Опустим из точки M перпендикуляр на сторону BC. Получим ME⊥BC. Тогда ΔBMA~ΔBEM по двум углам. Из подобия треугольников следует, что AB/BM=AM/ME.
Опустим из точки M перпендикуляр на сторону AD. Получим, MT⊥AD. Тогда ΔBMA~ΔATM по двум углам. Из подобия треугольников следует, что AB/AM=BM/MT, то есть AB/BM=AM/MT.
Так как AB/BM=AM/ME и AB/BM=AM/MT, то верно, что AM/ME=AM/MT или ME=MT.
Так как расстояния от точки M до прямых BC и AD одинаковы, то точка M лежит на средней линии трапеции.
Применив аналогичное рассуждение, получаем, что точка N тоже лежит на средней линии трапеции.
Тогда MN - это часть средней линии трапеции, то есть MN||BC и MN||AD.
Проведем среднюю линию трапеции FG. По определению FG=(7+12)/2=19/2.
Так как треугольники ΔBMA и ΔCND прямоугольные, а F и G - середины их гипотенуз AB и CD, то FM и GN - это медианы, равные AB/2 и CD/2 соответственно, то есть FM=5/2 и GN=4.
Понятно, что MN=FG-FM-GN, а значит MN=19/2-5/2-4=3.
Задача решена!
Відповідь:
128
Покрокове пояснення:
Вроде