Во 2 бочке было х л. мёда, в 1 бочке 5х л. , из первой забрал 51 л, а во вторую добавили 33 л. зная по условию задачи, чтопосле этого в бочках стало равное количество мёда, сост. ур-е: 5х-51=х=33
4х=33+51
х=84:4
х=21 л. мёда было во 2 бочке
5*21=105 л было в 1 бочке
2) -3(х+4)-5(2-3)=-3х-12-10+15=-3х-7
3)8,5х-2,15х=3,05х-9,5
6,35х-3,05х=-9,5
3,3х=-9,5
х=-9,5/3,3
х=-2,879
х+49=6(х-5)+2(х-6)
х+49=6х-30+2х-12
х-6х-2х=-30-12-49
-7х=-91
х=13
2 задание.
1)натуральные:
9, 24
2)целые:
9,-16,0,24,-50
3)положительные:
9; 1/19 ; 7,2; 4 3/16 ; 24
4)целые отрицательные:
-16, -50
5)дробные отрицательные:
-3,8; -2 6/17
Задание 3.
1)3,1> -6,7
2)-4,2> -4,6
Задание 4.
1)7,3+1,8-3,45 = 5,65 ( модуль раскрывается со знаком + )
2)17/90 : 1 8/9 = 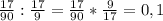
Задание 5.
1)если -х = 25,то х = -25
2)если -(-х)= - 4,9 , то х = -4,9
Задание 6.
1)модуль х = 4,5
х = ±4,5
2)модуль х = -1,8
Такого быть не может,т.к. любое число в модуле положительное,либо равно 0.
Задание 7.
х > -14
Наименьшее целое значение равно
x= -13
Задание 8.
-5,35* < -5,356
Вместо звездочки можно поставить цифры 5,4,3,2,1,0
Задание 9.
Нужно найти такие числа х,которые
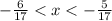
- 0,35294117647 < x < - 0,29411764705
Тогда х = - 0,34 и х = -0,33
36
Пошаговое объяснение:
Чтобы решить задачу, посмотрим, как устроен еженедельник из задачи. Его конструкция точно такая же, как и обычной ученической тетради. Берется несколько листов бумаги, по оси симметрии сцепляются скобками, и полученная пачка сгибается пополам. В результате, на 1 исходном листе получается 4 страницы, причем левый полулист по счету с начала, будет такой же как и правый полулист по счету с конца (в обратном направлении).
В нашей задаче на листе встречаются страницы с номерами 14 и 23, значит на этом же листе есть страницы №13 и №24 (т.к. начинается нумерация страниц с нечетного числа и заканчивается чётным). Очевидно, что 14 - это левая часть листа - полулист под номером 14:2=7.
Значит правая часть листа будет седьмой с конца.
Значит осталось еще правых 6 полулистов до конца еженедельника.
6 полулистов это 6*2=12 страниц.
24+12=36
Значит страница №36 - последняя в еженедельнике и всего их 36.
Задача решается именно для такой конструкции еженедельника, как указано выше. Для клеенного издания условие не подходит. т.к. на одном листе там обязательно будут соседние страницы.
№1.
Пусть Х меда было во 2 - ой бочке, тогда 5Х - было в 1 - ой бочке.
Зная, что когда из первой бочки забрали 51 л меда а в другой добавили 33 л меда и в бочках меда стало поровну, составим и решим уравнение:
5Х - 51 = Х + 33
5Х - Х = 33 + 51
4Х = 84
Х = 84 : 4
Х = 21
Значит, во 2 - ой бочке было 21 л меда, тогда в первой было: 21 * 5 = 105 л
ответ: 21 л; 105 л
№2
-3(Х+4)-5(2-3) = -3Х - 12 - 10 + 15 = -3Х - 7
ответ: -3Х - 7
№3
а)
8,5Х - 2,15Х = 3,05Х - 9,5
8,5Х - 2,15Х - 3,05Х = - 9,5
3,3Х = - 9,5
Х = - 9,5 : 3,3
Х = - 2,879
б)Х + 49 = 6(Х-5)+2(Х-6) = Х + 49 = 6Х - 30 + 2Х -12 = Х - 6Х - 2Х = - 30 - 12 - 49 =
-7Х = -91
Х = -91 : ( -7)
Х = 13
ответ: 13