Социология, социальная психология «Человек потому не поддается определению, что первоначально ничего собой не представляет. Человеком он становится лишь впоследствии, причем таким человеком, каким он сделает себя сам» (Ж.П. Сартр)
Индивид – это человек как отдельно взятый представитель общества. Ему присущи первичные потребности. Особенности же человека определяют его как личность. Я полностью согласна с высказывание Ж.П. Сартра о том, что изначально человек «ничего собой не представляет», а личностью он становится лишь в процессе социализации и самопознания. Потребности личности стоят на более высоких ступенях пирамиды Маслоу: потребность в общении, научном и культурном развитии. Подвергаясь влиянию окружающих его социальных групп и путем самоанализа, человек может самостоятельно сформировать себя как личность.
В подтверждение своей точки зрения хочу привести пример из жизни известного философа Иммануила Канта. Как известно, он родился болезненным ребенком, и врачи пророчили ему короткую жизнь. Но при силы воли и строгого самоконтроля Кант смог опровергнуть предсказания врачей. Его жизнь была долгой и насыщенной. Кроме того, философ посвятил себя изучению человеческого существования, что развитию не только его личности, но и всего человечества. Его трактаты людям осознать свое место в жизни.
Другой пример хотелось бы привести из литературы. Многие писатели подвергали своих героев духовным исканиям своего места в этом мире. К примеру, Евгений Онегин из романа А.С. Пушкина страдал от того, что не мог определить себя как личность. В нем не было исключительных особенностей, которые раскрывали бы его как субъекта социокультурной жизни.
Таким образом, можно сделать вывод, что слова Ж.П. Сартра справедливы во всех отношениях. Потребность в знаниях, культурном развитии, делает человека личностью.
7. 
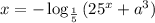
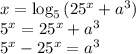
Пусть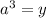 
, количество корней от этого не изменится.
Рассмотрим функцию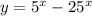 
:
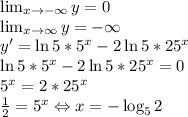
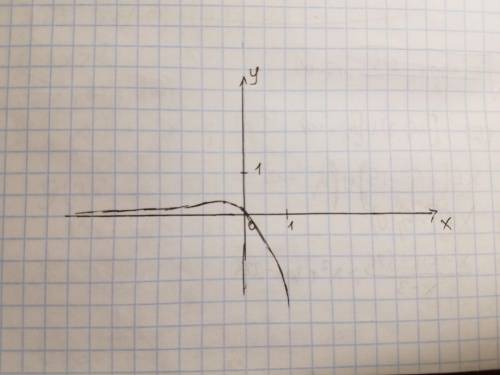
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно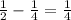 
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
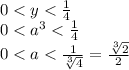
ответ: ![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
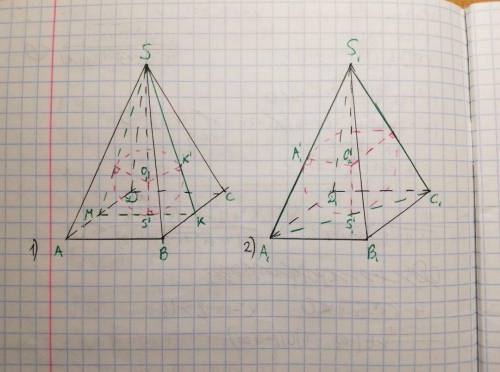
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
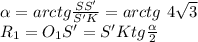
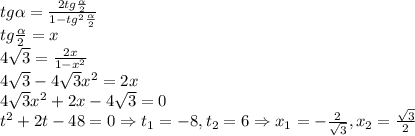
Учитывая, что угол находится в первой четверти,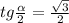 
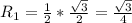
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
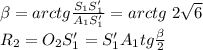
Решая аналогичное уравнение, получаем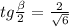 
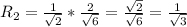
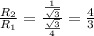
ответ: 4 : 3
Пошаговое объяснение:
(1.2a + 2.4b) - (4.3a + b) = 1.2a+2.4b-4.3a-b = -3.1a+1.4b