A. Сывосия нашла в лесу бревно длиной 12 м. Чтобы отнести домой, она распилила его на части длиной по 50 сантиметров. Сколько она сделала распилов? b. Из альбома Васосии выпал кусок, у первой страницы которого номер 31, а у последней — 114. Сколько страниц выпало?

c. У Совок несколько бревен. Они распили все бревна, сделав 19 распилов, и получили 34 куска. Сколько бревен было у Совок?
d. Мясистая сова по имени Ова хочет узнать. Сколько всего существует двузначных чисел? А трёхзначных?

e. Сов-сов надо подняться на столб высотой 10 км. Каждый день она поднимается на 4 км, а каждую ночь слетает на 3 км. Когда Сов-сов доберется до цели, если она стартовала в утром?

f. Главное здание Клювиков состоит из нескольких секторов. Этажи в разных секторах отличаются по высоте. Из-за этого, например, получается, что переходы с 12 этажа сектора Ова ведут на 17 этаж секторов Сов-сов и Васо. Как соотносятся по высоте этажи в этих секторах?
g. Сколько раз за сутки на часах Овоньки минутная стрелка обгонит часовую?
h. Для нумерации страниц в Овином блокноте Ове потребовалось 1249 цифр. Сколько страниц в блокноте Овы?
i. В ряд Сов-совия выписала все натуральные числа:
1234567891011121314151617181920...
Какая цифра стоит на 201986 месте?
j. Сыво купила тетрадь объемом 48 листов и пронумеровала все её страницы по порядку числами от 0 до 48. А Васо вырвала из этой тетради какие-то 35 страниц и сложила все 35 чисел, которые на них написаны. Могла ли у Васо получиться сумма 1118?

👇

Увидеть ответ

Ответ:

straikerfba

17.08.2020

а. 24 части это точно а дальше не читал

4,4(17 оценок)

Открыть все ответы

Ответ:

OwL505

17.08.2020

Решение.

1. Найдем производную функции f(x).

f'(x) = 3x^2 - 4x + 1.

2. Производная функции f(x) существует на всем числовом интервале.

3. Найдем стационарные точки функции f(x). Решим уравнение.

3x^2 - 4x + 1 = 0;

D = 16 - 12 = 4.

Уравнение имеет 2 корня х = 1/3 и х = 1.

4. Функция f(x) имеет 2 критические точки х = 1/3 и х = 1.

5. Исследуем критические точки на максимум и минимум.

Найдем вторую производную функции f(x).

f''(x) = 6x - 4.

f''(1/3) = 6 * 1/3 - 4 = -2 < 0. x = 1/3 - точка максимума.

f''(1) = 6 * 1 - 4 = 2 > 0. х = 1 - точка минимума.

ответ. Функция имеет 2 критические точки. х = 1/3 - точка максимума, х = 1 - точка минимума.

4,6(79 оценок)

Ответ:

67889055

17.08.2020

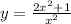Дано: $y = \frac{2x^2+1}{x^2}$ ;
Исследовать функцию и построить график.

Решение:

1) Функция не определена при обращении в ноль знаменателя, т.е. x ≠ 0 .

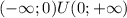D(f) ≡ R \ {0} ≡ $( -\infty ; 0 )U( 0 ; +\infty )$ ;

2) В функции встречаются только чётные степени аргумента, а значит она чётная. Докажем это:

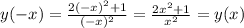$y(-x) = \frac{ 2(-x)^2 + 1 }{ (-x)^2 } = \frac{2x^2+1}{x^2} = y(x)$ ;

Найдём первую производную функции y(x) :

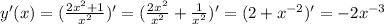$y'(x) = ( \frac{2x^2+1}{x^2} )' = ( \frac{ 2x^2 }{x^2} + \frac{1}{x^2} )' = ( 2 + x^{-2} )' = -2 x^{-3}$ ;

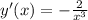$y'(x) = -\frac{2}{x^3}$ ;

При x = 0, производная y'(x) – не определена, как и сама функция, при всех остальных значениях аргумента функция и её первая производная определены и конечны, а значит функция непрерывная на всей области определения D(f) – на всей числовой прямой, кроме ноля.

3) Функция не определена при x = 0 . Это точка разрыва. При этом её значение стремится к положительной бесконечности, что легко доказать:

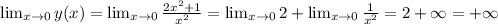$\lim_{x \to 0} y(x) = \lim_{x \to 0} \frac{2x^2+1}{x^2} = \lim_{x \to 0} 2 + \lim_{x \to 0} \frac{1}{x^2} = 2 + \infty = +\infty$ ;

Если приравнять функцию к нолю, получим:

y(x) = 0

;

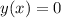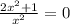$\frac{2x^2+1}{x^2} = 0$ ;

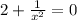$2 + \frac{1}{x^2} = 0$ ;

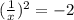$( \frac{1}{x} )^2 = -2$ – что невозможно ни при каких действительных значениях аргумента;

Значит, никаких пересечений графика с осями координат нет.

4. Найдем асимптоты y(x).

По найденному в (3) пределу, ясно, что линия x = 0 – является вертикальной двухсторонней асимптотой графика функции y(x) .

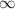Посмотрим, что происходит с функцией y(x) при устремлении аргумента к ± $\infty$ :

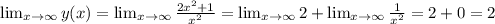$\lim_{x \to \infty} y(x) = \lim_{x \to \infty} \frac{2x^2+1}{x^2} = \lim_{x \to \infty} 2 + \lim_{x \to \infty} \frac{1}{x^2} = 2 + 0 = 2$ ;

Значит, уходя на бесконечность обоих знаков график функции y(x) имеет двунаправленную горизонтальную асимптоту y = 2 ;

Наклонных асимптот нет, и не может быть, так как есть горизонтальные с обеих сторон.

5. Первая производная функции y(x) :

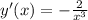$y'(x) = -\frac{2}{x^3}$ – положительна при отрицательных значениях аргумента и отрицательна при положительных х ;

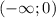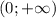Значит, функция возрастает на $( -\infty ; 0 )$ и убывает на $( 0 ; +\infty )$ ;

Уравнение y'(x) = 0

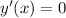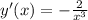т.е. $y'(x) = -\frac{2}{x^3}$ – не имеет решений, а значит, у функции нет экстремумов, т.е. конечных локальных минимумов или максимумов.

6. Найдём вторую производную функции y(x) :

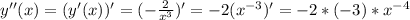$y''(x) = (y'(x))' = ( -\frac{2}{x^3} )' = -2 ( x^{-3} )' = -2*(-3)*x^{-4}$ ;

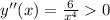$y''(x) = \frac{6}{x^4} 0$ при любых значениях аргумента ;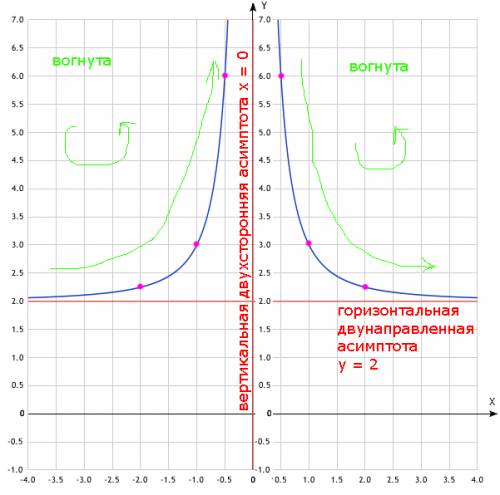

В силу общей положительности второй производной – график функции всегда «улыбается», т.е. он вогнут, или, говоря иначе: он закручивается против часовой стрелки на всём своём протяжении при проходе по числовой оси аргументов слева направо.

Поскольку выгнутость повсеместна, то и точек перегиба не может быть. И их нет, соответственно.

7.

При х = ± 1 : : : y(x) = 3 ;

При х = ± 2 : : : y(x) = 2.25 ;

При х = ± 1/2 : : : y(x) = 6 ;

Строим график:

Построить график построить график функции y = (2x^2+1)/x^2 по следующему алгоритму: 1) область опред