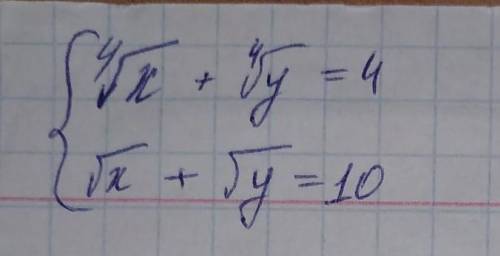
Y = x² - парабола (на рисунке синяя линия)
х = 3 - прямая перпендикулярная оси абсцисс, проходящая через точку (3,0) (зелёная линия на рисунке)
y = 0 - прямая, совпадающая с осью абсцисс (красная линия на рисунке)
Найдём ещё одну прямую, которая ограничивает параболу по иксу. Для этого в уравнение параболы подставляем y=0 и решаем уравнение относительно икса: x = 0 - ещё одна прямая перпендикулярная оси абсцисс (левая зелёная линия).
В итоге получается область серого цвета, площадь которой надо найти. Площадь находится с определённого интеграла от параболы в пределах от х=0 до х=3 (это будут пределы интегрирования).
Пошаговое объяснение:
Для удобства введём две замены: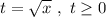 и
и 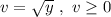 .
.
Решим верхнее уравнение системы отдельно.
Подкоренное выражение всегда неотрицательно.
Продолжаем решение уравнения.
Возведём обе части уравнения в квадрат.
Снова возведём обе части в квадрат.
По теореме Виета:
Подставляем каждое значение и находим
и находим 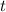 :
:
Обратная замена:
Данная система имеет две пары решений.
ответ: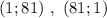 .
.