ответ: AB = BC = 24 см, MK = 37,6 см.
Пошаговое объяснение:
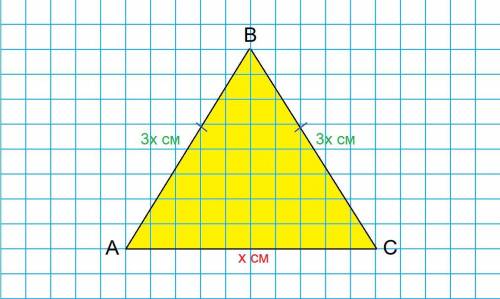
1) Пусть дан равнобедренный ΔABC.
Тогда AB и BC - боковые стороны, а AC - основание.
В равнобедренном треугольнике боковые стороны равны.
AB и BC - боковые стороны ⇒ AB = BC.
Пусть x см = AC, тогда AB = BC = 3x см.
Периметр ΔABC равен 56 см.
x + 3x + 3x = 56 ⇒ 7x = 56 ⇒ x = 8
8 см равно основание AC ⇒ AB = BC = 3 · 8 = 24 см.
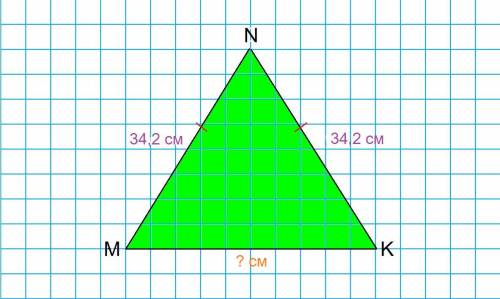
2) Пусть дан равнобедренный ΔMNK.
Тогда MN и NK - боковые стороны, а MK - основание.
В равнобедренном треугольнике боковые стороны равны.
MN и NK - боковые стороны ⇒ MN = NK = 31,2 см.
P ΔMNK = 1 м = 1 · 100 = 100 см.
⇒ MK = 100 - (31,2 + 31,2) = 100 - 62,4 = 37,6 см.
a) ab + ac + 2b + 2с = a) a(b+c) + 2(b+с) = (b+c)(a+2).
Стороны (b+c) и (a+2).
Модель изображена в прикреплённом изображении.
б) Eсли в условии описка, то решение такое:
х² + 2xy +y² = (х + у)²;
Квадрат со стороной (х+у).
в) Eсли в условии описка, то решение такое:
8y+cz + 8z + су = (8у+8z) + (сz+cy) = 8(y+z) + c(y+z) = (y+z)(8+c).
Стороны (у+z) и (8+с)