x ² =-3х+4 имеет два решения: x ₁ =1 и x ₂ =-4 .
. y=-3x+4 у=х²
х|-4|-1|0|1|4 x|-4|-1|0|1|4|
у|16|7|4|1|-8 y|16|1|0|1|16
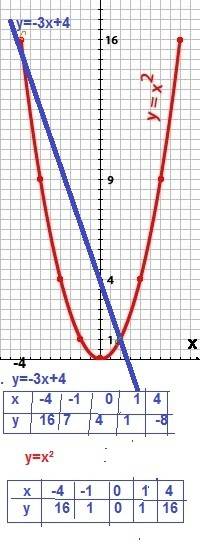
построим графики полученных функций см приложение
Точки пересечения прямой y = -3x+4 c параболой y = x ²
имеют координаты (1; 1) и (-4; 16)
Абсциссы этих точек и являются
решением нашего уравнения
x 1 =1 , x 2 =-4 .
Проверка x ²=–3x+4 подставим наши значения вместо х
1²=-3*1+4 верно
-4²=-3*(-4)+4 верно
записанное число делится на 81, следовательно оно делится и на 9. из признака делимости на 9 следует, что число единиц в этом числе так же делится на 9. среди чисел от 1 до 15 есть только одно такое число: 9, следовательно, в записи числа 9 единиц. данное число не делится на 10 и в его записи участвуют только нули и единицы, следовательно оно оканчивается на единицу. предположим, что можно вычеркнуть ноль так, чтобы оставшееся число делилось на 81. до вычеркивания нуля исходное число имело вид 10a+b, а полученное после вычеркивания a+b. преобразуем полученное число a+b=(10a+b)-9a 10a+b делится на 81 по условию. для того, чтобы a+b делилось на 81 нам необходимо, чтобы второе слагаемое делилось на 81, а для этого нужно, чтобы a делилось на 9 но этого не может быть так как число a записывается нулями и единицами, причем единиц не больше восьми, т.к. в исходном числе их было 9, причем одна из них находилась в самом правом разряде, т.е. неминуемо попала в число b. вывод: для числа a не выполнен признак делимости на 9, следовательно, 9a не делится на 81. противоречие.