1. A = {x| x∈N, (x+1)² < 27}
т.к. x - натуральное число, то x≥1, то x+1≥2>0,
(x+1)²< 27
5²=25<27 < 36 = 6²
т.к. x - натуральное, то имеем
0<x+1≤5,
1≤x≤4;
A = {1; 2; 3;4},
|A| = 4;
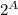= {∅, {1}, {2}, {3}, {4}, {1; 2}, {1; 3}, {1; 4}, {2; 3}, {2; 4}, {3; 4}, {1; 2; 3},
{1; 2; 4}, { 1; 3; 4}, {2; 3; 4}, {1; 2; 3; 4}}
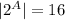
2. A = {0; 1; {2;3}}
B = {1; 2; 3}
C = {5; 6}
C-A = C\A = {5; 6},
A∩C = ∅,
B+C = BΔC = {1; 2; 3; 5; 6},
A - (B∪C) = A\(B∪C) = {0; 1; {2;3}}\{1; 2; 3; 5; 6} = {0; {2; 3}}.
3.
(A∩B)+(A∩C) = (A∩B)Δ(A∩C)
12 13/20 дм - периметр треугольника
Пошаговое объяснение:
6 1/5 дм - первая сторона
вторая сторона на 5 9/20 дм меньше первой:
6 1/5-5 9/20 = 31/5-109/20 = (31*4 - 109)/20 = (124 - 109)/20 = 15/20 = 3/4 дм - вторая сторона
5 7/10 дм - третья сторона
Периметр треугольника = сумме его сторон:
Р = 6 1/5 + 3/4 + 5 7/10 = 31/5 + 3/4 + 57/10 = (31*4+3*5+57*2)/20 =
(124+15+114)/20 = 253/20 = 12 13/20 (дм)