Для решения этой задачи надо немного пространственного воображения, чтобы понять, что высоту стола (Hст) можно выразить через рост Семёна (Hс) и рост Гриши (Hг). Итак, когда Семён стоит на столе, то разница между общим “ростом” (стола и Семёна) и ростом Гриши составляет 80 см, или математически: (Hст + Hс) - Hг = 80. А если Гриша стоит на столе, такая разница составит уже 100 см, т.е. (Hст + Hг) - Hс = 100. И тогда, понимая, что Hст, Hс и Hг — величины неизменные (на момент решения задачи), высоту стола можно определить, решив полученные равенства как систему, получив в итоге (Hст + Hс - Hг) + (Hст + Hг - Hс) = 80 + 100, откуда, раскрыв скобки и сгруппировав, имеем Hст + Hст + Hс - Hс + Hг - Hг = 180; 2×Hст = 180; Hст = 90 см. ответ: высота стола 90 см.
Поскольку весы именно чашечные, то задача нахождения фальшивой монеты из N сводится к бинарному поиску - мы каждый раз делим исходную кучку пополам (или на три части, если пополам не делится), определяем ту, которая легче, затем поступаем с ней аналогично. И т.д. пока сравнение не сведется к 2-м монетам - более легкая из них и есть искомая. При этом для N монет нам понадобится log2(N) взвешиваний. Если N не степень двойки, то округление идет до ближайшей СЛЕДУЮЩЕЙ. Т.о. в нашем примере log2(N) = 4. Откуда N = 2^4 = 16. 16 монет.
Решим систему методом сложения.
Складываем первое и второе уравнение системы.
Подставляем полученное значение в любое уравнение системы.
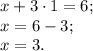
ответ: (3; 1).